Deep Dive into Data structures using Javascript - Linked List

What is a Linked List?

Linked List is a fundamental and linear data structure which is known for it’s high performance on insertion & deletion. It is commonly used as a building block in other data structures like Queues, Graphs and Trees. With that, we can also say Linked List is an important step to understand these data structures - as well as building custom ones.

There are different variations of Linked Lists: Singly Linked List (or we just say Linked List unless it is specified), Doubly Linked List, Circular Linked List, and more. For more details on variations, take a look at the Wikipedia page:

https://en.wikipedia.org/wiki/Linked_list

Among variations, Singly and Doubly Linked Lists are the most common ones. In this article we will be focusing on Singly Linked Lists.

Linked List in Javascript and other languages

Linked List is not a built-in data structure in Javascript, unlike Arrays and Hash Tables (Object, Map, Set). Programming languages like C++, Java, Clojure, Erlang, Haskell offers a built-in Linked List. Even though we don’t have a built-in implementation of Linked List in Javascript, we can build one - and that’s what we are going to do in this article.

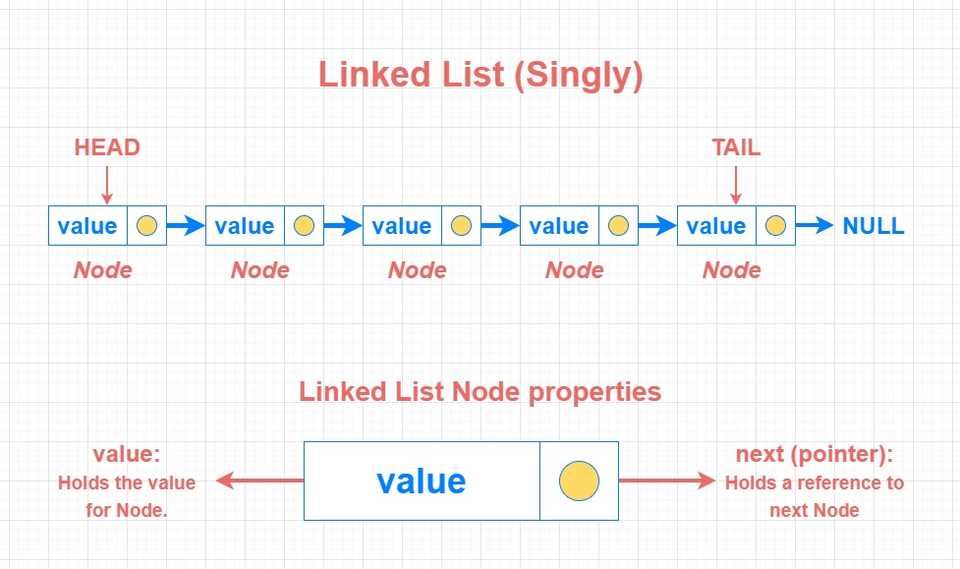
Anatomy of a Linked List

A Linked List is consisted by a series of connected Nodes. Each Node contains 2 properties:

Value: Holds the value / data for the Node.

Next (pointer): Holds a reference (pointer) to the next Node.

We also have specific names for the first and the last node in the list. We call the first node “HEAD” and the last node “TAIL”. As you see above, tail node points to a null value - which means Linked Lists are “null terminated”. In simpler words, this is how we know we are at the end of a Linked List.

When and When not to use Linked List

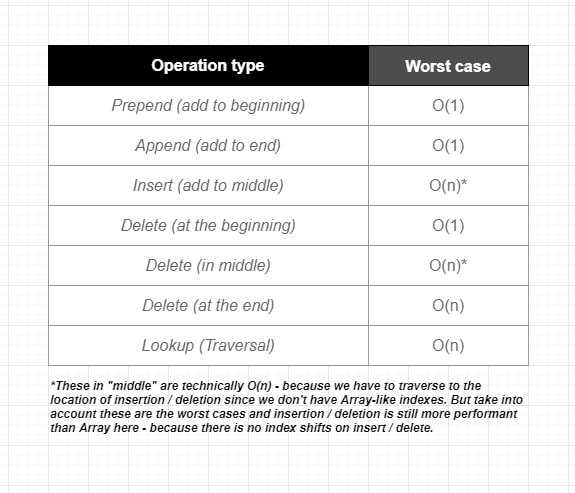
When you have a situation that you might want use a Linked List, often times the Array is the other option - and that’s what we are going to talk about in this section. But first, let’s start with taking a quick look at the Big O of common operations in Linked List:

Linked List vs Array

If this is your first time looking at Linked Lists, you are probably thinking “What is the point here? This looks somehow similar to an Array, both are some kind of a list at the end.” - this is what I thought at the first place as well. They have a similarity, because both Arrays and Linked Lists are in the same category which is called “Linear data structures”.

A linear data structure has their elements arranged linearly (or sequentially) - where each item has connection to it’s previous and next item. This connection makes it possible to traverse a linear data structure in a single level and a single run. Some other examples to Linear data structures are Stacks and Queues.

Even they are in the same category, they still have some specific differences. To understand that, we need to look at how their data is stored inside the actual memory. Because that’s the point having a direct consequence on how efficiently we can interact with the data. When we are aware of that, we can make an educated decision on which data structure would suit best for the problem that we want to solve.

Main difference between a Linked List and an Array is indexes. Arrays are indexed while Linked Lists are not. For example, we can directly pick an element from an Array by using it’s index:

const fruits = ["apple", "watermelon", "strawberry"]

fruits[2] // picks "strawberry"

Picking an element with it’s index is very fast, because the index directly points to the memory address of the value. To pick an element from a Linked List, we need to make a traversal through the list until we find the target value (or until the tail if not found) - since there is no indexes but list of pointers.

Wait a minute - What does even “Traversal” mean?

”Traversal” or ”Lookup” is a commonly used term in Computer Science, which is often interchangeably used and confused with ”Iteration”. In fact, Iteration is actually a type of Traversal that is discrete - in simpler words it is a finite loop (goes through the items a fixed number of times). Every iteration is a traversal, but not every traversal is an iteration.

Since Linked Lists does not have a fixed number of items, that is why we use the word Traversal instead of Iteration.

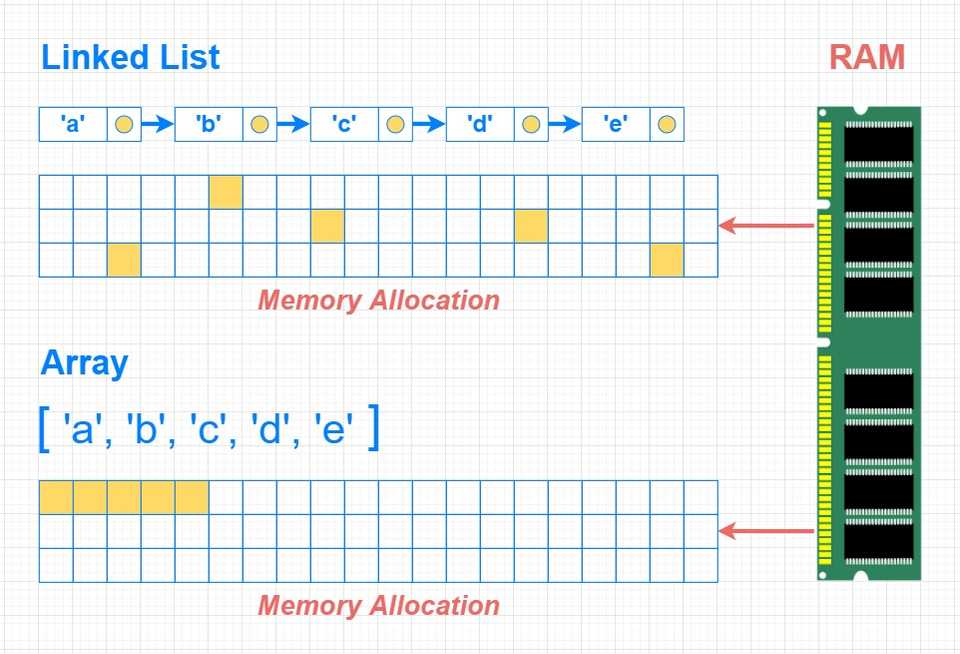
Difference between Linked List and Array in memory

If we take a look at the visual below, you will see the Array elements being stored sequentially in a contiguous memory location, while Linked List elements are all over the place (similar to Hash Tables). Even they are not in a contiguous memory location, we are still able to use it as a list - because the next (pointer) property we have inside each node makes it possible to know what is the next element whenever we traverse through it.

Linked List advantages over Array:

Better performance on inserting a value at the beginning of the list (also called Prepend). When we do this in an Array, all upcoming indexes will be shifted - which costs O(n) Linear time. But since Linked Lists doesn’t have indexes, there is no need to shift anything. All we do is changing the reference of pointer. With Linked Lists, Prepend costs O(1) Constant time.
Better performance on deleting an item at the beginning of the list - similar to Prepend. Costs O(1) Constant time while it costs O(n) Linear time with Arrays.
Better performance on inserting or deleting a value at the middle of a list - this is correct if you somehow maintain pointer references somewhere for quick lookup, for example in an Hash Table. When that is the case, complexity will be O(1), because all we do is shifting pointers. But the base implementation is technically O(n) because we have to traverse to the location of insertion / deletion since we don’t have indexes. This is also O(n) in Arrays and it may seem like the same thing - but let’s not forget there is a part which effects the speed here: traversal speed between Arrays and Linked Lists.

Traversal is way much slower on Linked List compared to Arrays, due to how it’s data is physically stored in memory like we seen above. Even though changing pointer references costs much less than index-shifting on surface, when we add the traversal the cost in terms of time will be much more. Therefore an Array can outperform Linked List due to it’s traversal speed.
Linked Lists are not fixed size, can expand and shrink during runtime (compared to Static Arrays)
Memory Allocation for Linked Lists are done during runtime, there is no need to allocate fixed memory (compared to Static Arrays)

Linked List disadvantages over Array:

Slower access due to not having indexes. To retrieve an item traversal is needed. Arrays have O(1) Constant time on Access while on Linked List is O(n) Linear time.
It needs more memory than arrays since it is holding a pointer inside each node.
Traversal is slower than Arrays, because elements are all over the place in memory unlike Arrays where the elements are placed in a contiguous block.
Traversing from reverse order is not possible on Singly Linked Lists unlike Arrays (but it is possible for Doubly Linked Lists).

Use Linked Lists over Arrays when:

You need high performance on insert & delete at the beginning of the list. Because you don’t have to worry about the performance loss on index-shifts Arrays have.
You don’t need to use Random Access (directly access an element by using it’s index).
You want to build Queue data structure (they can be built with Arrays or Linked Lists). Linked List is a better choice here, because Linked list is a more performant option on FIFO (First In First Out) type of operations - because we need to work at the beginning of the list when removing items.
You don’t need to do traversal very often (traversal here is slightly slower than Array, due to not having contiguous Memory Allocation)

Do not use Linked List over Arrays when:

You don’t need to make a lot of insertions at the beginning of list.
You need to use Random Access (directly access an element by using it’s index).
You want to build Stack data structure (which can be also built with Arrays or Linked Lists). Arrays are a simple and straightforward choice for LIFO (Last In First Out) type of operations - because we only work at the end of the list when removing items.
You need to do traversals very often (traversal is more performant than Linked Lists, due to having contiguous Memory Allocation).

Linked List implementation in Javascript

Now we have a good foundation about the anatomy of Linked List, it is time to actually build one. We will be using ES6 Classes to build our Linked List - it is a very convenient tool for the use case. I’d also like to encourage you to open your favorite code editor and follow along with me as we go through the steps.

To have a first look, this is how a Linked List output looks like in Javascript code:

{
  head: {
    value: 10,
    next: {
      value: 15,
      next: {
        value: 20,
        next: {
          value: 25,
          next: null
        }
      }
    }
  },
  tail: { value: 25, next: null }
  length: 4 // length is optional
}

What we see is a lot of nested Objects - which makes sense since the Objects are reference types in Javascript.

Step 1 - Build a class for the Linked List Node

Let’s start with identifying the main building block: which is the Node element. We can use a class for it, so we can call it whenever we need to create a new Node.

// Define Node class:
class Node {
  constructor(value, next) {
    this.value = value
    this.next = next
  }
}

// Create a new Node:
const newNode = new Node(10, null)
console.log(newNode)

/* newNode output:
Node {
  value: 10,
  next: null
}
*/

Step 2 - Build a class for the Linked List

As the next step, we can go further and create the LinkedList class. We know that there should be head and tail properties. For ease of use, we can as well add a length property to keep track of our list length.

Additionally, we can have an option in the constructor to create the Linked List empty or with a single starter value. We will be looking at the append method at the next step.

class LinkedList {
  constructor(value) {
    this.head = null
    this.tail = null
    this.length = 0
  }

  // make it optional to create Linked List with or without starter value
  if (value) {
    this.append(value)
  }
}

const linkedList = new LinkedList()
console.log(linkedList)

/* linkedList output at initializing stage (empty starter):

LinkedList {
  head: null,
  tail: null,
  length: 0
}

*/

At this point we are done with the base building blocks: Node and LinkedList classes. We can continue with extending our class by introducing common methods. Here is the list of methods we are going to implement:

append(value) - add to the end
prepend(value) - add to the beginning
toArray() - return Linked List elements in an array for ease of debugging
traverseToIndex(index) - traversal helper
insert(index, value) - add to the middle
deleteHead() - delete from beginning
deleteTail() - delete from the end
delete(index) - delete from the middle
reverse() - reverse order of items

Step 3 - Linked List append method

linkedlistappendgif-visualgo

To implement the append method, we follow these steps:

Check if list is empty. If it is empty, assign the newNode to both head and tail.
If list is not empty, assign the newNode to this.tail.next, after that assign the newNode to this.tail.
Increment the length by 1, return the Linked List using “this”:

append(value) {
    // Initialize a newNode with value recieved and next as null.
    const newNode = new Node(value, null)
    
    // Let's check if Linked List is empty or not first.
    if (!this.head) {
      // If there is no head (no elements) it is empty. In that case make the newNode as head
      // since it is the only node at this point and there is no tail either,
      // tail will also have the same value (both head and tail will point to same place in memory from now on):
      this.head = newNode
      this.tail = newNode
    } else {
      // If Linked List is not empty, Attach new node to the end of linked list:
      // extend list by using tail.next (both head and tail points to same place)
      this.tail.next = newNode
      // now reset the tail by placing the latest inserted node:
      this.tail = newNode
    }

    this.length++
    return this
  }

linkedList.append(10)
linkedList.append(15)

/* Output: 
LinkedList {
  head: Node { value: 10, next: null },
  tail: Node { value: 10, next: null },
  length: 1
}

LinkedList {
  head: Node {
    value: 10,
    next: Node { value: 15, next: null }
  },
  tail: Node { value: 15, next: null },
  length: 2
}

*/

Hold on, what is going on with the head and tail? How can `this.tail.next` can change the value of `this.head`?

Confused? That’s perfectly normal, it is a bit tricky at first time. But no worries - before moving onto next methods, let’s clear up the confusion about what is actually going on with HEAD and TAIL here.

We will look into both steps in detail - appending when list is empty and appending when there is elements in the list.

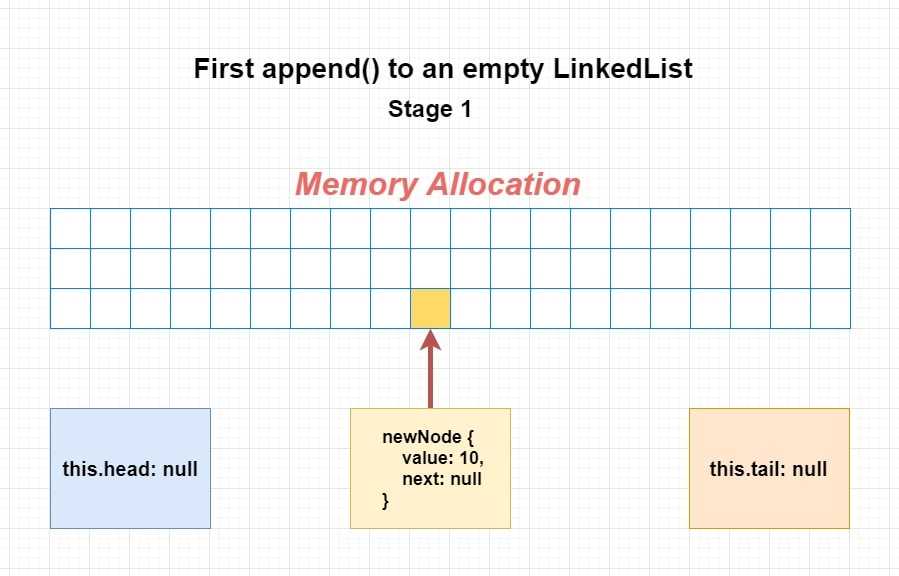
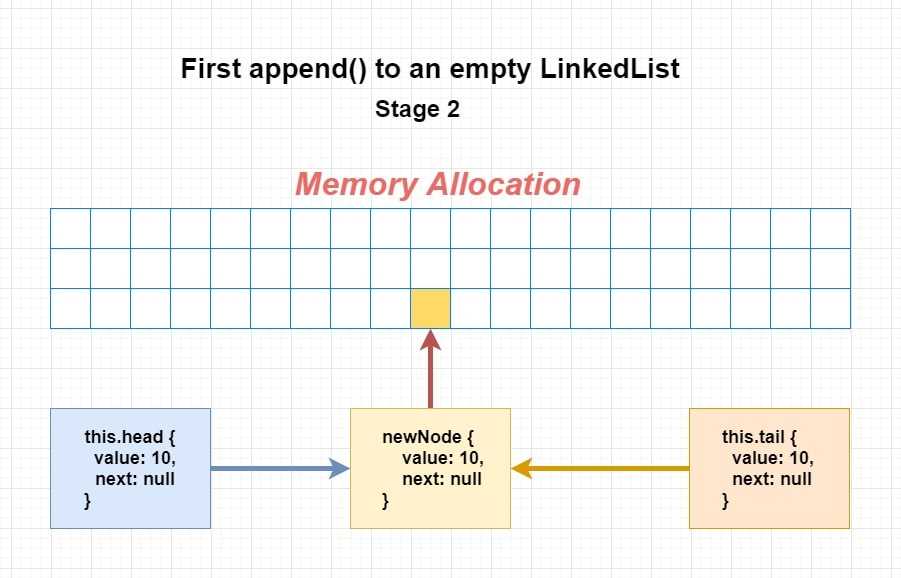
Part 1 - Append to empty Linked List

Stage 1: We always start with creating a newNode with the value we recieve. At this point, newNode is in the memory and head & tail is still null:

append(value) {
  const newNode = new Node(value, null)
  ...
}

Stage 2: Since it is the first Node, both HEAD and TAIL will have the same value at this point of time. To do that, we assign the newNode to this.head and this.tail:

append(value) {
  const newNode = new Node(value, null)

  if (!this.head) {
    this.head = newNode
    this.tail = newNode
  } else {
    ...
  }
    ...
  }
    
linkedList.append(10)

When we do this, both head and tail points to the same place in memory - which is the place of newNode:

Part 2 - Append to non-empty Linked List

Stage 1: Now let’s assume we will append another element after having at least one element in the list. To do that, we first assign the newNode to this.tail.next

append(value) {
  const newNode = new Node(value, null)

  if (!this.head) {
    ...
  } else {
      this.tail.next = newNode
      ...
  }
    ...
}
  
linkedList.append(15)

Since both head and tail points to same place, assigning newNode to this.tail.next also effects the this.head.next. At this point, our Linked List looks like this:

LinkedList {
  head: Node {
    value: 10,
    next: Node {
      value: 15,
      next: null,

    }
  },
  tail: Node {
    value: 10,
    next: Node {
      value: 15,
      next: null,
    }
  },
  length: 2,
}

Stage 2: As we know, tail always contains the latest element. Since we are appending (adding to the end of list) here, we want to make sure tail only contains the latest appended Node. That’s why we use this.tail = newNode right after this.tail.next = newNode here:

append(value) {
  const newNode = new Node(value, null)

  if (!this.head) {
    ...
  } else {
      this.tail.next = newNode
      this.tail = newNode
  }
    ...
}
  
linkedList.append(15)

Now when we print the our list at this step, it will look like this instead:

LinkedList {
  head: Node {
    value: 10,
    next: Node {
      value: 15,
      next: null,

    }
  },
  tail: Node {
    value: 15,
    next: null
  },
  length: 2,
}

I hope this shed some light on how head and tail interacts inside the Linked List - because this is a key concept to understand how Linked List methods actually work. It is not just limited to how append method works, you will see this similar pattern in other methods as well.

Step 4 - Linked List prepend method

linkedlistprependgif-visualgo

// Add to the beginning of list
  prepend(value) {
    // Initialize a newNode with value recieved and next as null.
    const newNode = new Node(value, null)
    // Assign this.head to newNode.next property. Because we are adding to the beginning - and this newNode's next should be pointing to this.head.
    newNode.next = this.head
    // Now that newNode has the this.head as "next", we can set the this.head as newNode directly.
    this.head = newNode
    this.length++
  }

Step 5 - Linked List toArray method (optional)

To easily debug what is going on our list (or have an option to output Linked List as an array), we will need toArray method:

// toArray - loop through nested objects, then return the values in an array
  toArray() {
    const array = []
    // Initialize a currentNode variable pointing to this.head - which will be the starting point for traversal.
    let currentNode = this.head

    // fill the array until we reach the end of list:
    while (currentNode !== null) {
      array.push(currentNode.value)
      currentNode = currentNode.next
    }
    return array
  }

Step 6 - Linked List traverseToIndex method (helper)

Since both insert and removal related methods will have to deal with traversing to a specific index, it will be wise to implement a helper for it:

// lookup / traversal helper
traverseToIndex(index) {
  // Validate the received index parameter:
  if (typeof index !== 'number') return 'Index should be a number'
  if (index < 0) return 'Index should be 0 or greater'

  // keeps track of traversal
  let counter = 0
  // starting point
  let currentNode = this.head

  // traverse to the target index
  while (counter !== index) {
    currentNode = currentNode.next
    counter++
  }

  return currentNode
}

Step 7 - Linked List insert method

linkedlistinsertgif-visualgo

// Add by specifying index (to the middle)
insert(index, value) {
  // Validate the received index parameter:
  if (typeof index !== 'number') return 'Index should be a number'
  if (index < 0) return 'Index should be 0 or greater'

  // if length is too long, just append (add to the end)
  if (index >= this.length) {
    return this.append(value)
  }

  // if length is 0, just prepend (add to the beginning)
  if (index === 0) {
    return this.prepend(value)
  }

  // Initialize a newNode with value recieved and next as null.
  const newNode = new Node(value, null)

  // pick previous index
  const preIdx = this.traverseToIndex(index - 1)
  // pick target index
  const targetIdx = preIdx.next
  // place newNode in front of previous node
  preIdx.next = newNode
  // place target index in front of new node
  newNode.next = targetIdx
  this.length++
}

Step 8 - Linked List deleteHead method

linkedlistdeleteheadgif-visualgo

deleteHead() {
  // check if there is a head value - if not return a warning (or an error)
  if (!this.head) return 'List is empty'

  const headVal = this.head.value

  // if one element left
  if (this.head === this.tail) {
    this.head = null
    this.tail = null
    this.length--
    return this
  }

  // define newHead as this.head.next
  const newHead = this.head.next
  // now change the head pointer to newHead
  this.head = newHead
  this.length--
  return headVal
}

Step 9 - Linked List deleteTail method

linkedlistdeletetailgif-visualgo

deleteTail() {
  // check if length is zero - if not return a warning (or an error)
  if (!this.head) return 'List is empty'

  const tailVal = this.tail.value

  // If there is only one node left
  if (this.head === this.tail) {
    this.head = null
    this.tail = null
    this.length--
    return tailVal
  }

  // Traverse to the last node, delete the next pointer on previous node of tail
  let currentNode = this.head
  while (currentNode.next) {
    if (!currentNode.next.next) {
      currentNode.next = null
    } else {
      currentNode = currentNode.next
    }
  }

  // Update the tail node:
  this.tail = currentNode
  this.length--
  return tailVal
}

Step 10 - Linked List delete method

linkedlistdeletegif-visualgo

delete(index) {
  // Validate the received index parameter:
  if (typeof index !== 'number') return 'Index should be a number'
  if (index < 0) return 'Index should be 0 or greater'

  // Handle the case if there is 2 elements left - in this case we either remove head or tail:
  if (this.length === 2) {
    if (index === 0) {
      return this.deleteHead()
    }
    if (index > 0) {
      return this.deleteTail()
    }
  }

  // For a list with more than 2 elements, define removal style. 
  // Removal will be either from head, middle or tail.
  let removalType
  if (index === 0) {
    removalType = 'head'
  } else if (index >= this.length) {
    removalType = 'tail'
  } else {
    removalType = 'middle'
  }

  if (removalType === 'head') {
    return this.deleteHead()
  }

  if (removalType === 'tail') {
   return this.deleteTail()
  }

  // To remove from middle, we will need both previous and target nodes
  if (removalType === 'middle') {
    const preIdx = this.traverseToIndex(index - 1)
    const targetIdx = preIdx.next
    const targetVal = targetIdx.value
    // Implement removal by pointing preIdx.next to targetIdx.next
    // This will detach the target index node from Linked List
    preIdx.next = targetIdx.next
    this.length--
    return targetVal
  }
}

NOTE: When we remove the pointer from a value in the object, it gets garbage collected (removed from memory) - this is due to garbage collection feature of JS engine.

Final step - Linked List reverse method

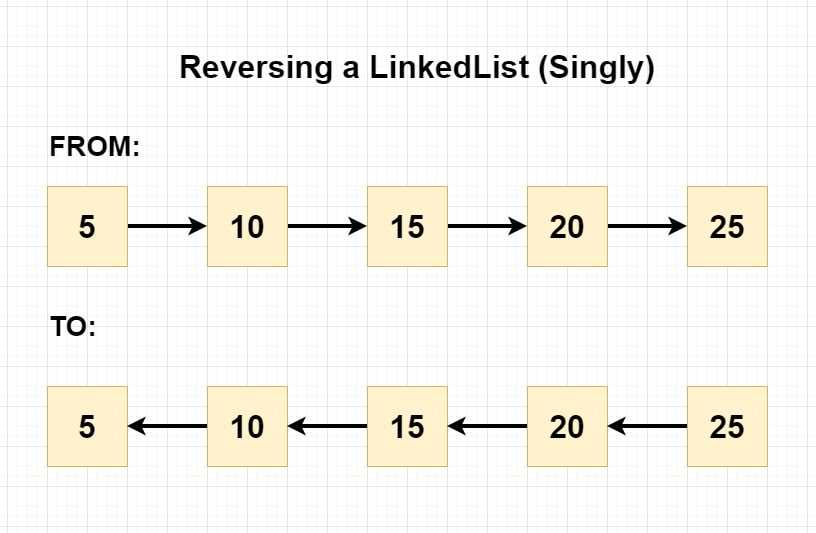
This method is an absolute classic when it comes to technical interviews, you will probably face this one day if you haven’t yet: “Can you reverse a Linked List?”

No worries - we will figure it out while implementing this method.

To reverse the Linked List, we follow these steps:

As a first step check if the list only contains one item. In that case no need to reverse it, we simply return.
If there is more than one item, we are going to reverse the list. To be able to do that, we will need to use 3 pointers:
- previousNode (null at the start)
- currentNode
- nextNode (null at the start)

Why do we even need 3 pointers?

What we want to do here is basically changing the directions of all pointers:

As an example, we can take a look at first 3 elements: 5 -> 10 -> 15

If we point the nextNode’s next back to the first Node, we will lose the pointer to the third element - in other words we will break the list:

5 <- 10 15

To be able to continue, we also need to save a reference to the next - that way we can keep moving forward while reversing the pointers on each step:

5 <- 10 <- 15

reverse() {
  // Checkup - if list only contains one item, no need to reverse
  if (!this.head.next) return

  // We'll use 3 pointers. Prev and Next is empty at the start
  let previousNode = null
  let currentNode = this.head
  let nextNode = null

  while (currentNode !== null) {
    // Start with taking the next node reference
    nextNode = currentNode.next
    // Then, point the currentNode to previous one
    currentNode.next = previousNode
    // Now, move the previous and current one step forward. How?
    // To move the previousNode one step forward, we reference it to the currentNode:
    previousNode = currentNode
    // To move the currentNode one step forward, we reference it to the nextNode:
    currentNode = nextNode
  }

  // set the new tail with this.head (it contains the last item at this point of time):
  this.tail = this.head
  // now reference this head to previousNode (contains the reversed list):
  this.head = previousNode
  return this
}

It was a lot to take in - but I hope this article helped you to understand how the Linked Lists works! I’d also like to encourage you to check out this amazing data structures and algorithms visualizer (I have actually generated the gifs you have seen above at this website): https://visualgo.net/en

You can see the full implementation of the Linked List in Javascript that we went through in this article below. Thanks for reading!

Implementation of Linked List in Javascript:

class Node {
  constructor(value, next) {
    this.value = value
    this.next = next
  }
}

class LinkedList {
  constructor(value) {
    this.head = null
    this.tail = null
    this.length = 0

  // make it optional to create linked list with value or empty
  if (value) {
    this.append(value)
  }
  }
  
  append(value) {
    // Initialize a newNode with value recieved and next as null.
    const newNode = new Node(value, null)
    
    // Let's check if Linked List is empty or not first.
    if (!this.head) {
      // If there is no head (no elements) it is empty. In that case make the newNode as head
      // since it is the only node at this point and there is no tail either,
      // tail will also have the same value (both head and tail will point to same place in memory from now on):
      this.head = newNode
      this.tail = newNode
    } else {
      // If Linked List is not empty, Attach new node to the end of linked list:
      this.tail.next = newNode      
      this.tail = newNode
    }

    this.length++
  }
  
  // Add to the beginning of list
  prepend(value) {
    // Initialize a newNode with value recieved and next as null.
    const newNode = new Node(value, null)
    // Assign this.head to newNode.next property. Because we are adding to the beginning - and this newNode's next should be pointing to this.head.
    newNode.next = this.head
    // Now that newNode has the this.head as "next", we can set the this.head as newNode directly.
    this.head = newNode
    this.length++
  }
  
  // toArray - loop through nested objects, then return the values in an array
  toArray() {
    const array = []
    // Initialize a currentNode variable pointing to this.head - which will be the starting point for traversal.
    let currentNode = this.head

    // fill the array until we reach the end of list:
    while (currentNode !== null) {
      array.push(currentNode.value)
      currentNode = currentNode.next
    }
    return array
  }
  
  // lookup / traversal helper
  traverseToIndex(index) {
    // Validate the received index parameter:
    if (typeof index !== 'number') return 'Index should be a number'
    if (index < 0) return 'Index should be 0 or greater'

    // keeps track of traversal
    let counter = 0
    // starting point
    let currentNode = this.head

    // traverse to the target index
    while (counter !== index) {
      currentNode = currentNode.next
      counter++
    }

    return currentNode
  }
  
  // Add by specifying index (to the middle)
  insert(index, value) {
    // Validate the received index parameter:
    if (typeof index !== 'number') return 'Index should be a number'
    if (index < 0) return 'Index should be 0 or greater'

    // if length is too long, just append (add to the end)
    if (index >= this.length) {
      return this.append(value)
    }

    // if length is 0, just prepend (add to the beginning)
    if (index === 0) {
      return this.prepend(value)
    }

    // Initialize a newNode with value recieved and next as null.
    const newNode = new Node(value, null)

    // pick previous index
    const preIdx = this.traverseToIndex(index - 1)
    // pick target index
    const targetIdx = preIdx.next
    // place newNode in front of previous node
    preIdx.next = newNode
    // place target index in front of new node
    newNode.next = targetIdx
    this.length++
  }
  
  deleteHead() {
    // check if there is a head value - if not return a warning (or an error)
    if (!this.head) return 'List is empty'

    const headVal = this.head.value

    // if one element left
    if (this.head === this.tail) {
      this.head = null
      this.tail = null
      this.length--
      return headVal
    }

    // define newHead as this.head.next
    const newHead = this.head.next
    // now change the head pointer to newHead
    this.head = newHead
    this.length--
    return headVal
  }
  
  deleteTail() {
    // check if length is zero - if not return a warning (or an error)
    if (!this.head) return 'List is empty'

    const tailVal = this.tail.value

    // If there is only one node left
    if (this.head === this.tail) {
      this.head = null
      this.tail = null
      this.length--
      return tailVal
    }

    // Traverse to the last node, delete the next pointer on previous node of tail
    let currentNode = this.head
    while (currentNode.next) {
      if (!currentNode.next.next) {
        currentNode.next = null
      } else {
        currentNode = currentNode.next
      }
    }

    // Update the tail node:
    this.tail = currentNode
    this.length--
    return tailVal
  }
  
  delete(index) {
    // Validate the received index parameter:
    if (typeof index !== 'number') return 'Index should be a number'
    if (index < 0) return 'Index should be 0 or greater'

    // Handle the case if there is 2 elements left - in this case we either remove head or tail:
    if (this.length === 2) {
      if (index === 0) {
        return this.deleteHead()
      }
      if (index > 0) {
        return this.deleteTail()
      }
    }

    // For a list with more than 2 elements, define removal style. 
    // Removal will be either from head, middle or tail.
    let removalType
    if (index === 0) {
      removalType = 'head'
    } else if (index >= this.length) {
      removalType = 'tail'
    } else {
      removalType = 'middle'
    }

    if (removalType === 'head') {
      return this.deleteHead()
    }

    if (removalType === 'tail') {
     return this.deleteTail()
    }

    // To remove from middle, we will need both previous and target nodes
    if (removalType === 'middle') {
      const preIdx = this.traverseToIndex(index - 1)
      const targetIdx = preIdx.next
      const targetVal = targetIdx.value
      // Implement removal by pointing preIdx.next to targetIdx.next
      // This will detach the target index node from Linked List
      preIdx.next = targetIdx.next
      this.length--
      return targetVal
    }
  }
  
  reverse() {
    // Checkup - if list only contains one item, no need to reverse
    if (!this.head.next) return

    // We'll use 3 pointers. Prev and Next is empty at the start
    let previousNode = null
    let currentNode = this.head
    let nextNode = null

    while (currentNode !== null) {
      // Start with taking the next node reference
      nextNode = currentNode.next
      // Then, point the currentNode to previous one
      currentNode.next = previousNode
      // Now, move the previous and current one step forward. How?
      // To move the previousNode one step forward, we reference it to the currentNode:
      previousNode = currentNode
      // To move the currentNode one step forward, we reference it to the nextNode:
      currentNode = nextNode
    }

    // set the new tail with this.head (it contains the last item at this point of time):
    this.tail = this.head
    // now reference this head to previousNode (contains the reversed list):
    this.head = previousNode
    return this
  }
}

Published Dec 15, 2021