Deep Dive into Data structures using Javascript - Circular Queue (Ring Buffer)

What is a Circular Queue / Ring Buffer?

Circular Queue, which can be also called as Ring buffer, Cyclic buffer or Circular Buffer is a variation of Queue data structure where the last element is connected to the first element to form a circle. It supports FIFO (First In First Out) order of operations exactly like the regular Queue, but it has a few key differences:

• Circular Queue always has finite size, unlike the Linear (regular) Queue. Because Linear Queue can be initialized as bounded/finite or unbounded/infinite size. Circular Queue gets initialized with the given number to set the fixed capacity to determine the maximum number of items it can hold.
• It is more memory efficient compared to the bounded / fixed capacity Linear Queue due to circular usage. Because when we remove items from a fixed capacity Linear Queue that is already at its maximum size, these items will create empty spaces at the front of the Queue that cannot be reused. Since it is used in a linear fashion, the tail pointer never goes back to the front of the Queue.

Circular Queue has 2 variations: Blocking and Non-blocking. These are related to how Circular Queue behaves when it reaches its maximum capacity.

• With the Blocking variation, we cannot insert another item unless we remove an item.
• With the Non-blocking variation, the next insertion at the max capacity overwrites the oldest inserted value. Evicted (removed) value can be received from the Circular Queue by using a callback function.

Circular Queue is not a built-in data structure in Javascript, but we can implement a custom one.

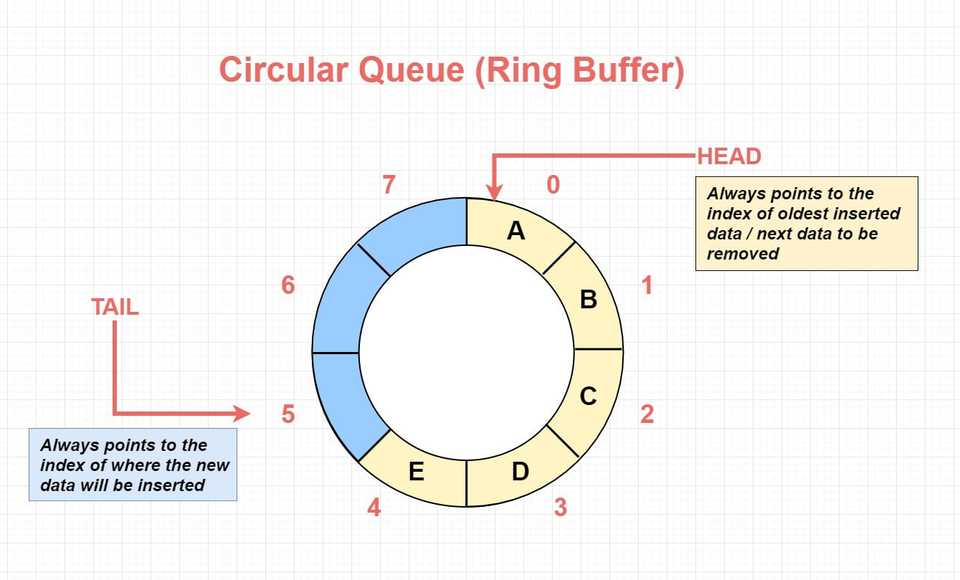
Anatomy of a Circular Queue

Circular Queue follows the FIFO (First In First Out) order of operations like a Queue, but in a circular manner. It can be implemented using an Array or a Linked List, but the most common and most straight-forward implementation is the Array version - and we will be focusing on this variation in this article.

We will use an Array to hold Circular Queue items, and will maintain head and tail pointers to be able to achieve the circular manner.

Head: Always points to the index of oldest inserted data / next data to be removed.

Tail: Always points to the index of where the new data will be inserted

This data structure may remind you of the Circular Linked List. But the difference is we do not store pointers in every element here. So how do we achieve the circular manner then?

Here is how: we track the size of Queue and only store the head and tail as pointers to relevant Array indexes. Then update their positions accordingly on additions and removals by using the power of modulo arithmetic via modulo operator - which is very useful to deal with circular logic.

Did it sound complicated? It probably is right now, but no worries - we will take a closer look when we come to the implementation section.

When to use Circular Queue

Circular Queue shares the same Big O complexity with Queue data structure. And the reason we may want to consider choosing this data structure is very similar to the reasons we want to use a Queue - where we want to enforce FIFO (First In First Out) rule of access. For more details, please refer to the section “When to use Queue” in the article: Queue

When you have a situation that you might want to use a Circular Queue, often times the choice is between Linear (regular) Queue and Circular Queue. So when you should choose Circular Queue over Linear Queue?

• You know the number of items that you are going to operate with / or have a little amount of memory available to use. Because Circular Queue is more memory efficient compared to the Linear Queue.
• You want to have a circular manner in your operations.

Apart from Queue specific use cases, Circular Queues are used in many applications in the real world:

• Used in buffering data streams.
• Used in audio processing.
• Producer Consumer problem, where Circular Queue helps to solve synchronization problems between different processes.
• Traffic lights that are connected to computer controlled traffic systems, and more.

Circular Queue implementation in Javascript

As I have mentioned earlier, we will be using an Array to build this data structure. The key underlying concept to fully understanding how Circular Queue operates is the usage of the Modulo operator. So let’s see how the Modulo operator will help us to achieve the circular manner in this data structure.

What is the Modulo operator and how does it work exactly?

Simply put, Modulo operator is used to representing Modulo - which is a mathematical operation that gives the remainder after a division of 2 integers. This holds true as long as both numbers are positive. Even though we won’t be dealing with the negative numbers in the case of Circular Queue, it’s definitely an important rule that is good to remember. With that cleaned up, let’s continue with Modulo operator cases with only positive numbers:

Example

If we divide 10 by 3, we get 3 times 3, then 1 is left as a remainder. And that’s the number we get when we use the Modulo operator:

10 = 3 x 3 + 1 --- remainder is 1

This is where the Modulo operator comes in as a shortcut:

10 = 3 x 3 + 1 --- remainder is 1 ---> 10 % 3 = 1
10 = 4 x 4 + 2 --- remainder is 2 ---> 10 % 4 = 2
10 = 5 x 5 + 0 --- remainder is 0 ---> 10 % 5 = 0
....

In the above example, first number was always bigger than the second number. You maybe wondering how does Modulo operator work if the first number is smaller than the second number. Let’s revert the values of the above example:

3 = 10 x 0 + 3 --- remainder is 3 ---> 3 % 10 = 3
4 = 10 x 0 + 4 --- remainder is 4 ---> 4 % 10 = 4
5 = 10 x 0 + 5 --- remainder is 5 ---> 5 % 10 = 5
....

This may look a bit confusing, but no worries - we just learned the second rule: If the first number is less than the second number in a Modulo operation, we always return the first number. But why? Let’s take a closer look focusing on a single example:

• 3 = 10 x 0 + 3 --- remainder is 3 ---> 3 % 10 = 3
• Why do we multiply 10 with 0? Because there is no 10 in the 3, so it ends up as 0.
• And since this is an equation that is supposed to be equal to 3 at the end, we simply return the first number.

You may be wondering at this point, shouldn’t we get 0 as a remainder after dividing 3 by 10, because 3 divided by 10 equals 0.3? Not in this case, because we are dealing with integers, Modulo operator won’t return anything that includes fractions or decimals.

If you are using another language than Javascript, another key point to note here is Modulo operators can work differently depending on the programming language. So if the Modulo definition is not the same as Javascript in the language you are using, there is a possibility you may not get the same result from the Modulus logic in the examples I will be sharing below. If you want to dive deeper into this, I’d suggest you check this Wikipedia article:

https://en.wikipedia.org/wiki/Modulo_operation#In_programming_languages

I believe we have a solid foundation on how to deal with the Modulo operator by now. Let’s get back to the Circular manner part. We can start by seeing it in action with a simpler example:

// Print all days of the week twice using a single array.

const days = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday']

function circulateList(arr, times) {
  const iterationAmount = arr.length * times

  for (let i = 0; i < iterationAmount; i++) {
    console.log(
      `Day: ${arr[i % arr.length]} - Modulo operation: ${i} % ${arr.length} = ${i % arr.length}`
    )
  }
}

circulateList(days, 2)

// OUTPUT:

'Day: Monday - Modulo operation: 0 % 7 = 0'
'Day: Tuesday - Modulo operation: 1 % 7 = 1'
'Day: Wednesday - Modulo operation: 2 % 7 = 2'
'Day: Thursday - Modulo operation: 3 % 7 = 3'
'Day: Friday - Modulo operation: 4 % 7 = 4'
'Day: Saturday - Modulo operation: 5 % 7 = 5'
'Day: Sunday - Modulo operation: 6 % 7 = 6'
'Day: Monday - Modulo operation: 7 % 7 = 0'
'Day: Tuesday - Modulo operation: 8 % 7 = 1'
'Day: Wednesday - Modulo operation: 9 % 7 = 2'
'Day: Thursday - Modulo operation: 10 % 7 = 3'
'Day: Friday - Modulo operation: 11 % 7 = 4'
'Day: Saturday - Modulo operation: 12 % 7 = 5'
'Day: Sunday - Modulo operation: 13 % 7 = 6'

As you see above, even though we had an array with 7 elements, we were able to iterate it 14 times in a single loop thanks to the Modulo operator. This means every time we get to the end of an array, we can automatically start from zero - and that’s the use case we want to have with Circular Queue.

As we know from the start of the article, there are 2 variations of Circular Queue: Blocking and Non-blocking. I will be sharing both implementations below along with gifs to visualize how the pointers move around as we do additions (enqueue) and removals (dequeue). We will be using an ES6 Class to build both variations of this data structure. Here is the list of methods in the implementations:

CircularQueueBlocking(capacity: number)

• enqueue(value) - add to the end of Queue.
• dequeue() - remove from the beginning of Queue
• peek() - retrieve the first element in the Queue
• isFull() - helper method to check if Queue is at maximum capacity
• isEmpty() - helper method to check if Queue is empty
• length() - optional method to check the length of Queue
• clear() - optional method to clear the Queue
• toArray() - optional method returns Queue elements as an Array

CircularQueueNonBlocking(capacity: number, evictionCallback: function)

It includes all methods from Blocking Circular Queue, plus an additional helper method:

• _rotateHead() - helper method for overwriting the oldest item in the Queue

Additionally it also accepts an optional callback function in it’s constructor: evictionCallback. This can be useful if we want to retrieve the oldest value every time an overwrite occurs in the Circular Queue.

I hope this article helped you to understand what Circular Queue is and how it works! I’d like to encourage you to experiment with the implementations below in your favorite code editor. Thanks for reading!

Blocking Circular Queue visualizations:

enqueue():

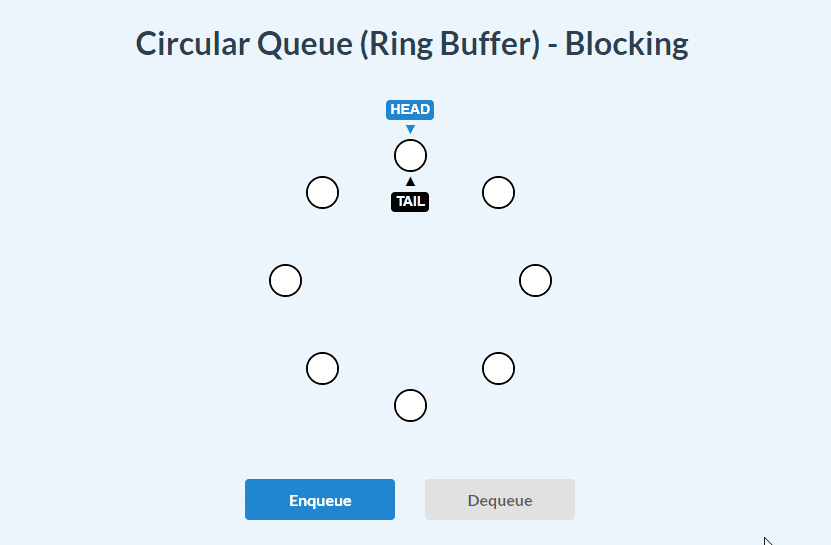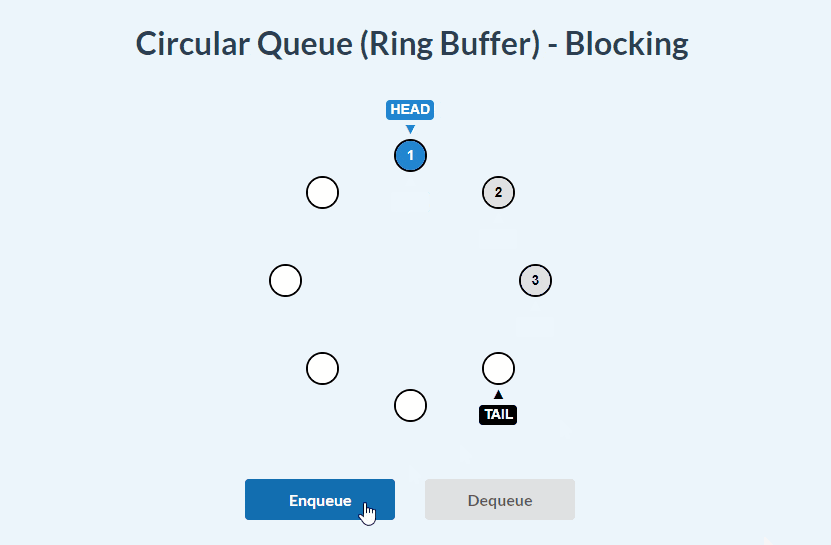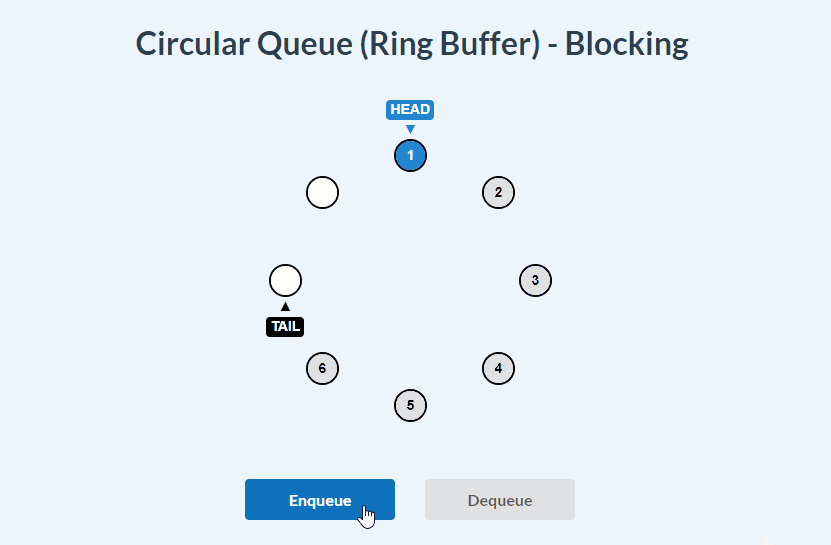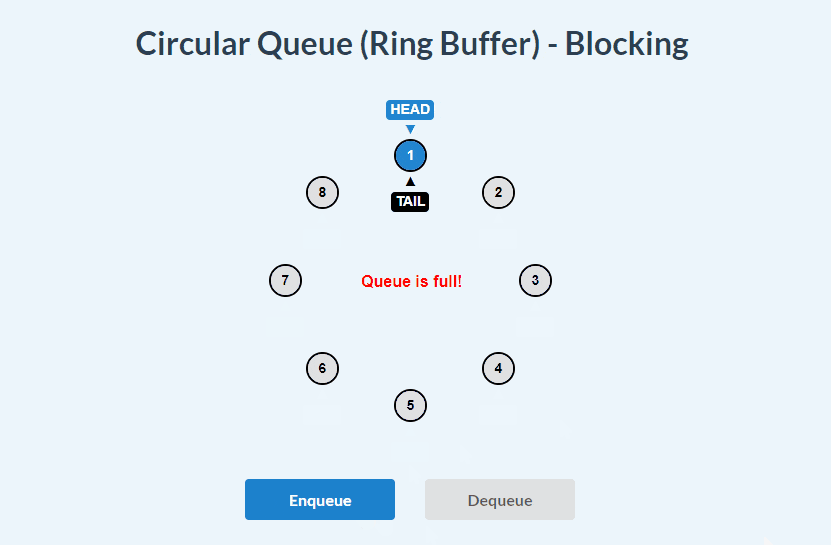
dequeue():

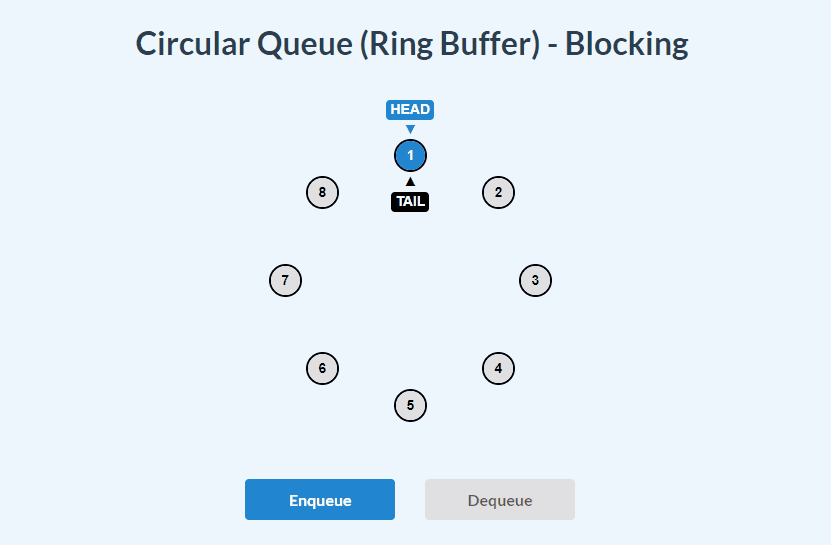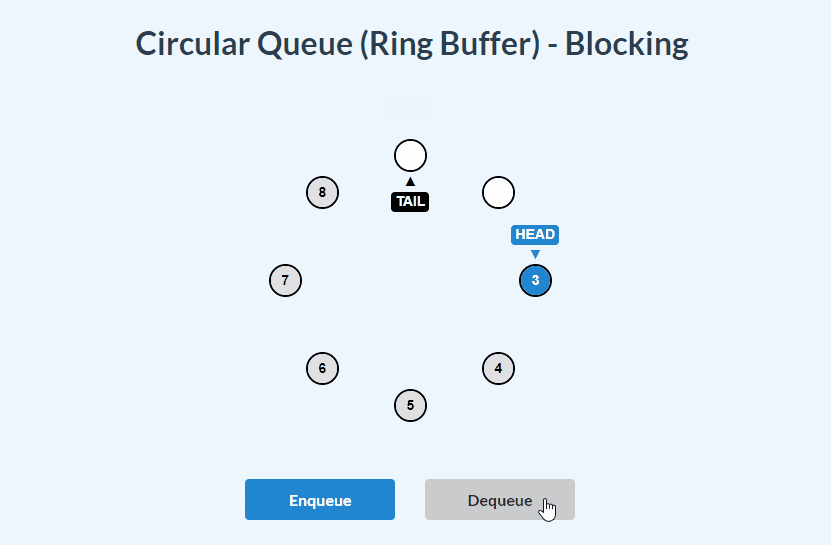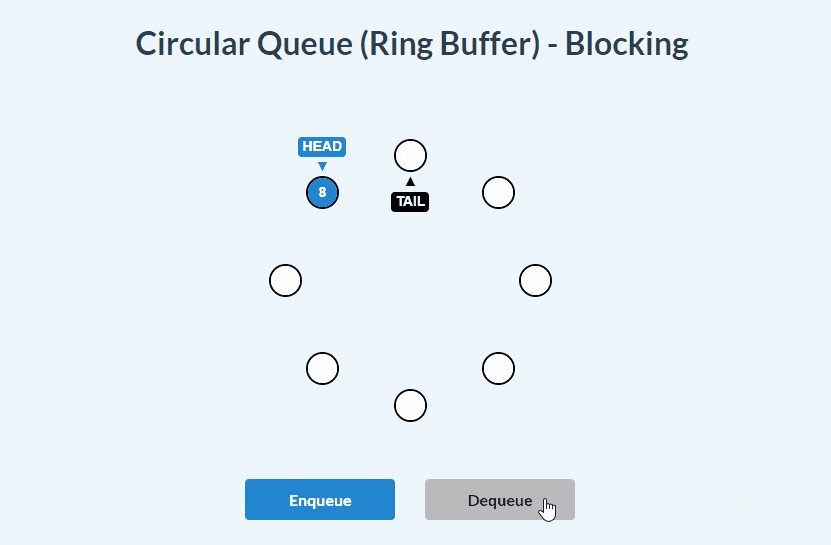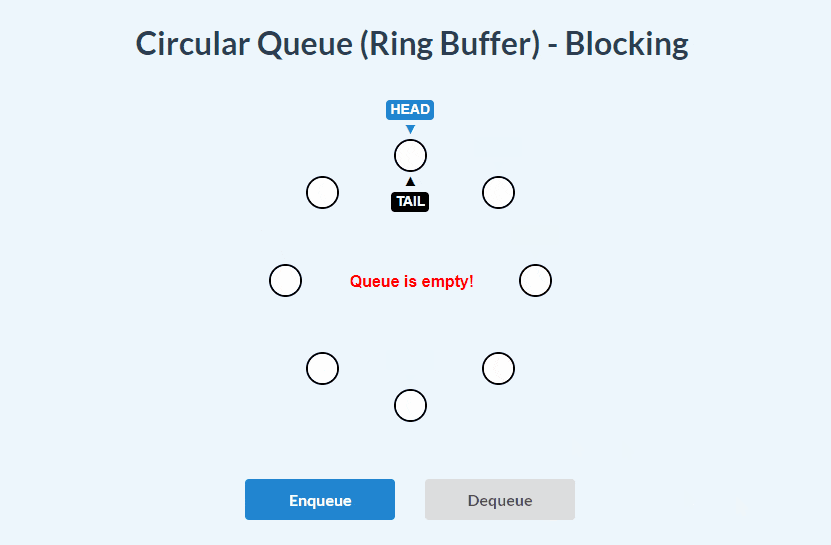
enqueue() and dequeue():

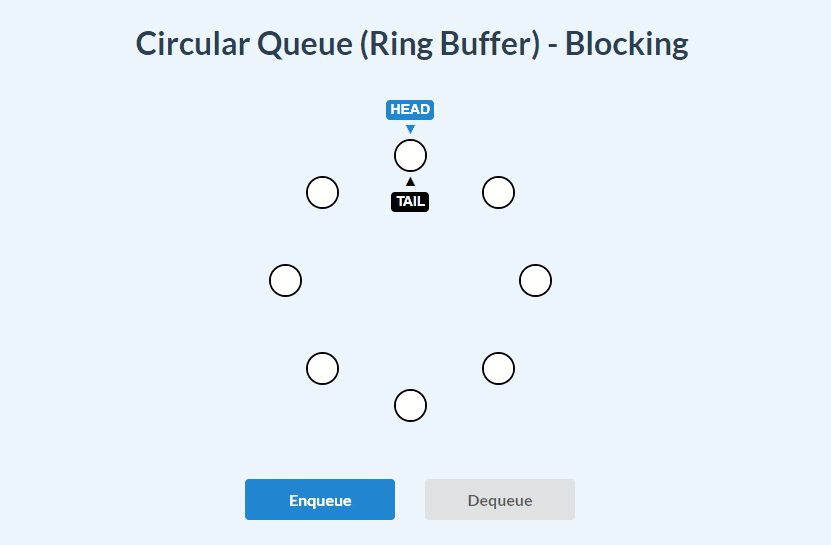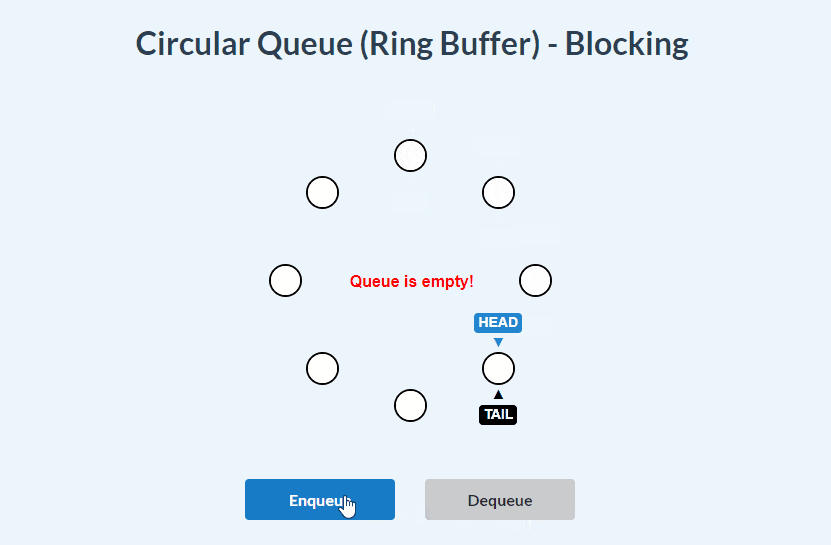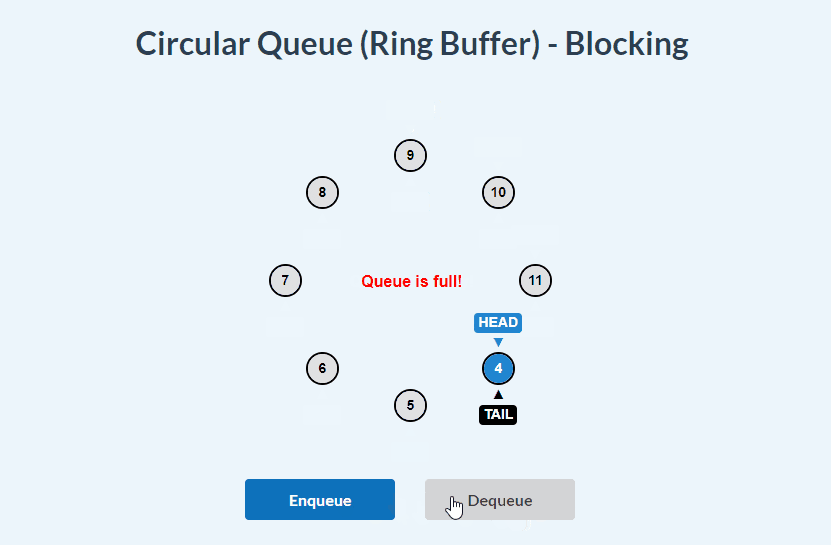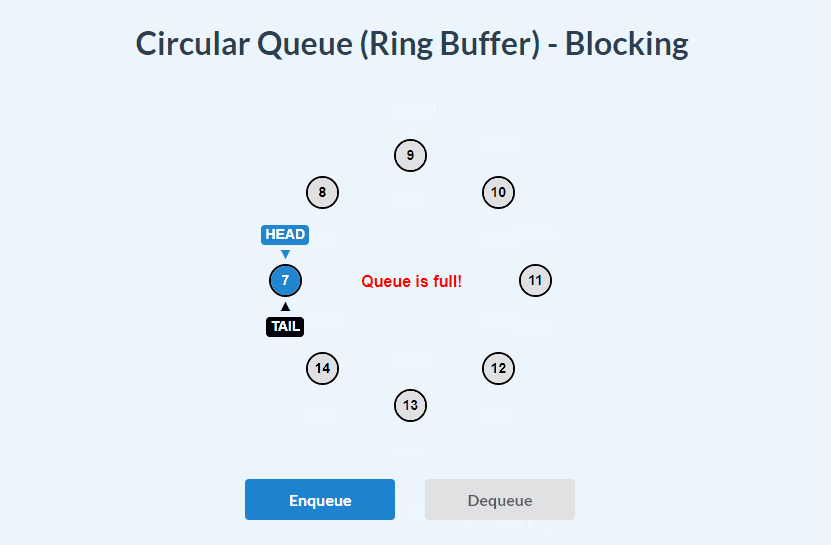
Blocking Circular Queue implementation:

class CircularQueueBlocking {
  constructor(capacity) {
    // Validate capacity
    if (typeof capacity !== 'number' || capacity < 1) {
      throw new Error('Please specify capacity of the Queue')
    }
    
    this.head = 0
    this.tail = 0
    this.size = 0
    this.items = Array.from({ length: capacity })
    this.capacity = capacity
  }
  
  enqueue(item) {
    if (this.isFull()) {
      throw new Error('Queue is full!')
    }
    this.items[this.tail] = item
    this.tail = (this.tail + 1) % this.capacity
    this.size++
  }
  
  dequeue() {
    if (this.isEmpty()) 
      throw new Error('Queue is empty!')
    
    // store the item about to be removed:
    const removedItem = this.peek()
    
    // set the current head to be undefined (remove)
    this.items[this.head] = undefined
    
    // move the head index by 1 using modulus operator:
    this.head = (this.head + 1) % this.capacity    
    this.size--
    return removedItem
  }
  
  peek() {
    return this.items[this.head]
  }
  
  isFull() {
    return this.capacity === this.size
  }
  
  isEmpty() {
    return this.size === 0
  }
  
  length() {
    return this.size
  }
  
  clear() {
    this.items = []
    this.head = 0
    this.tail = 0
    this.size = 0
  }
  
  toArray() {
    return this.items
  }
}

Non-Blocking Circular Queue visualizations:

enqueue():

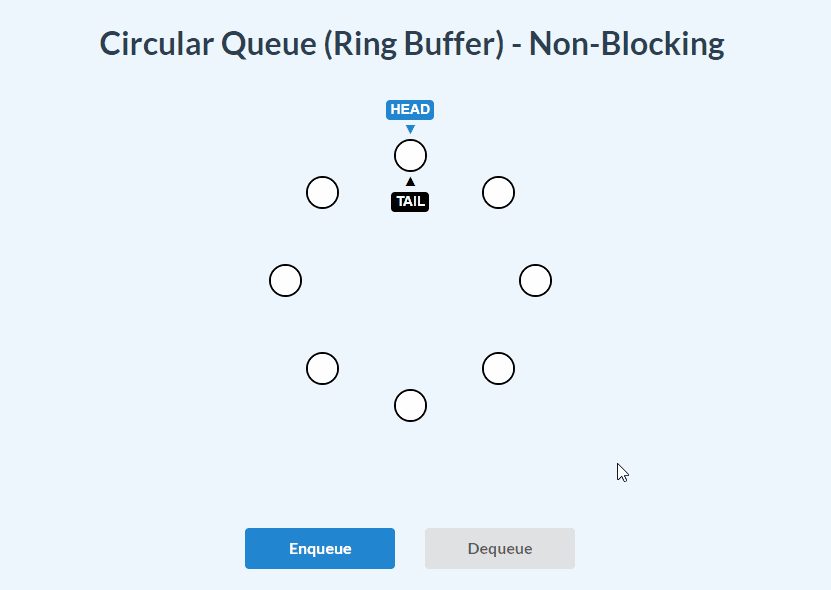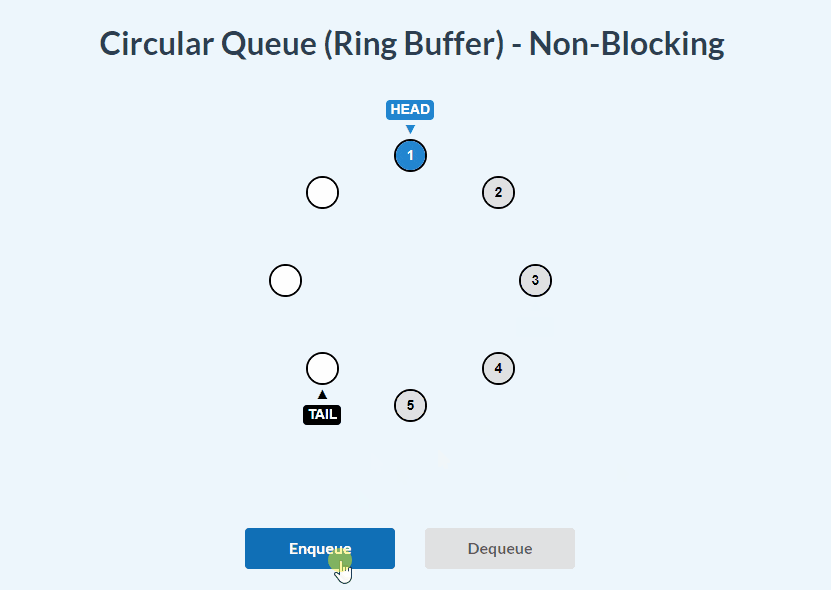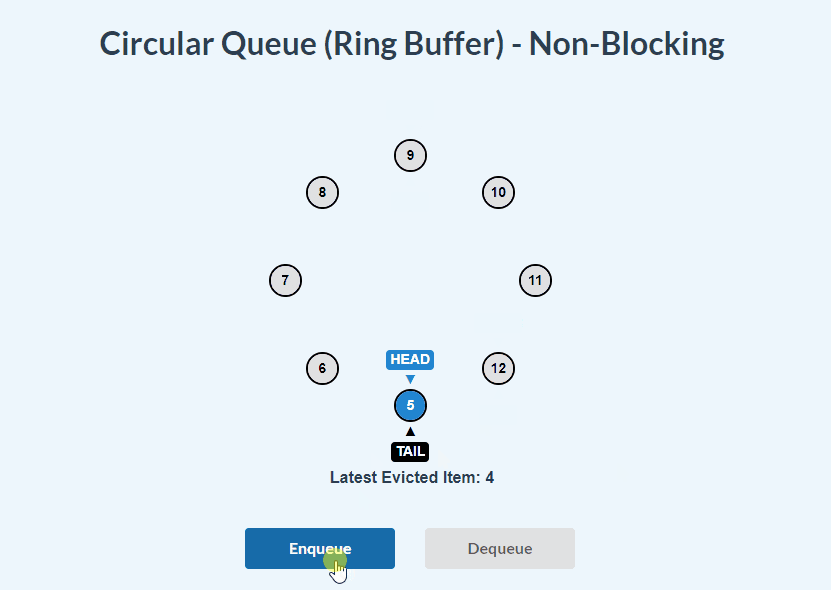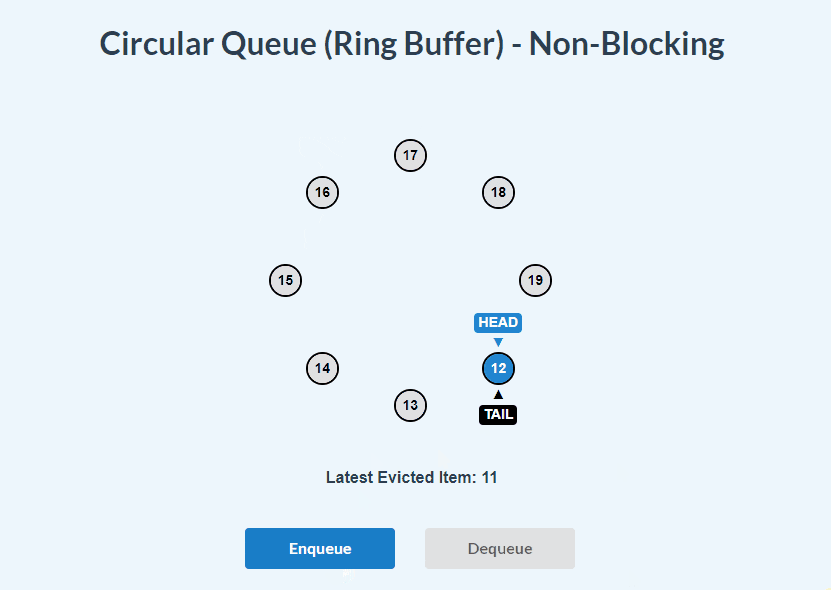
dequeue():

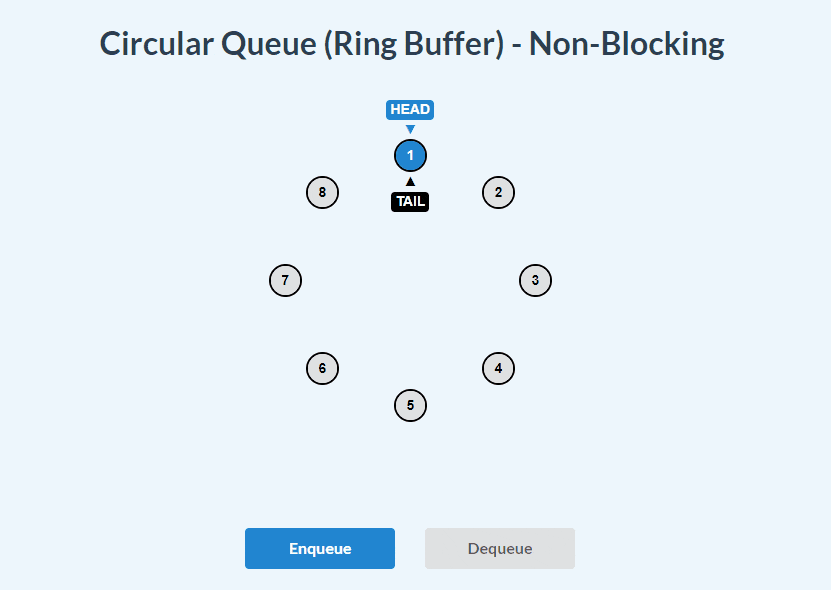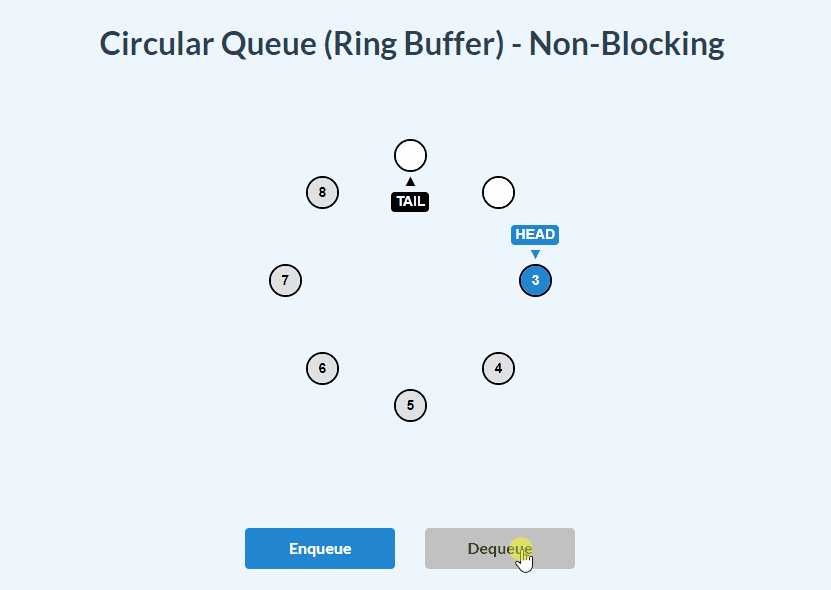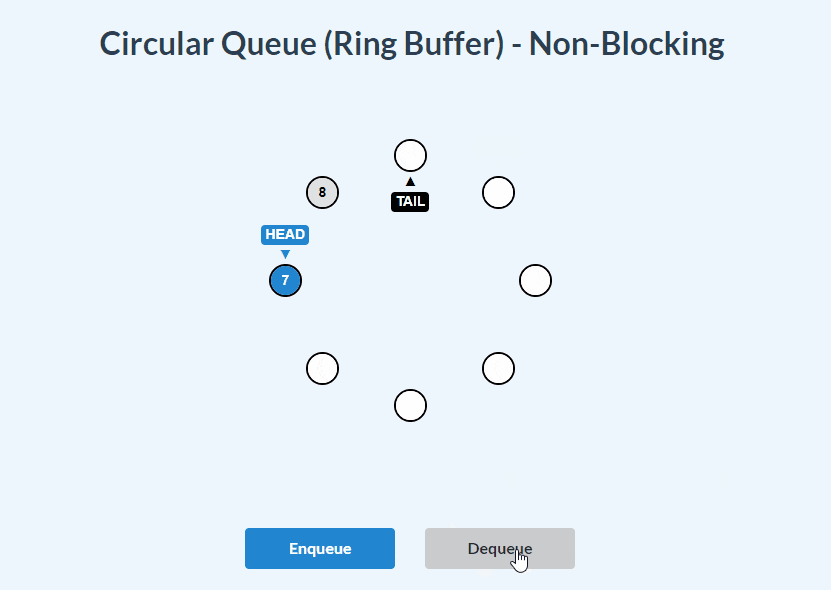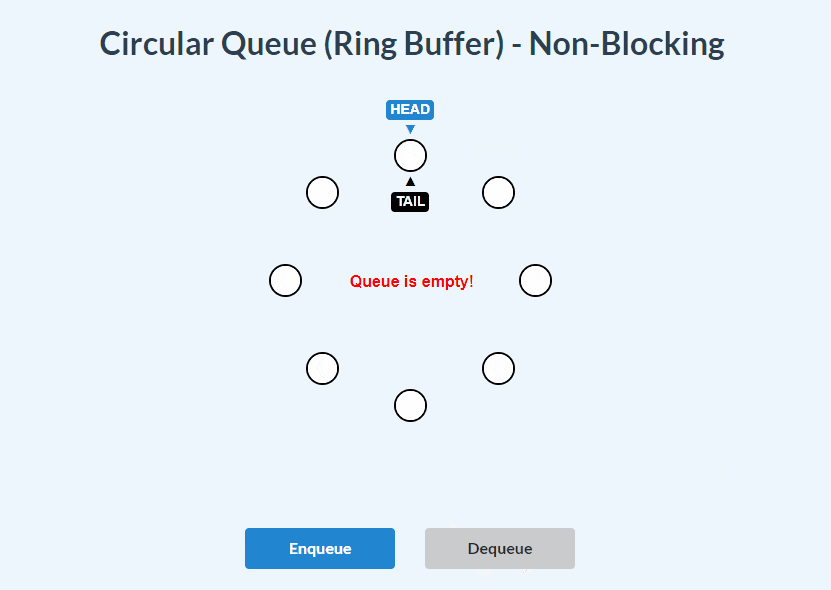
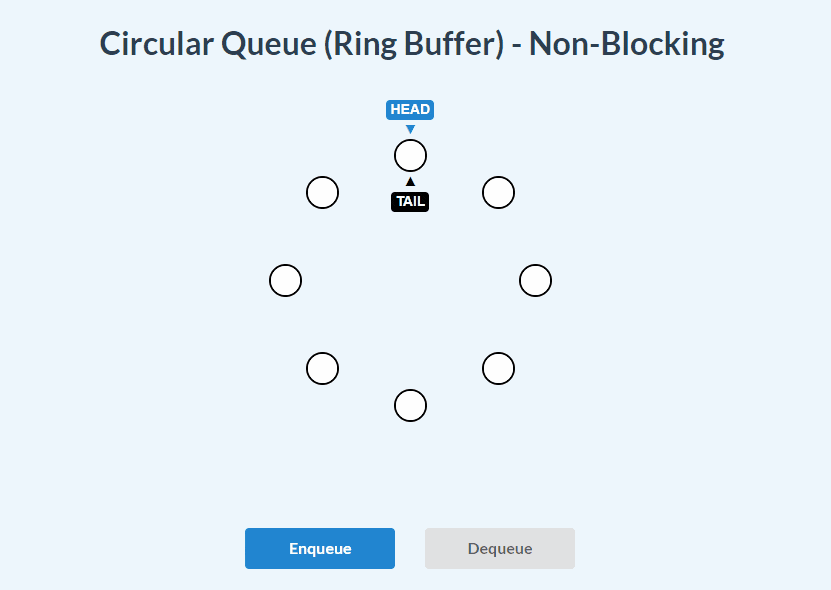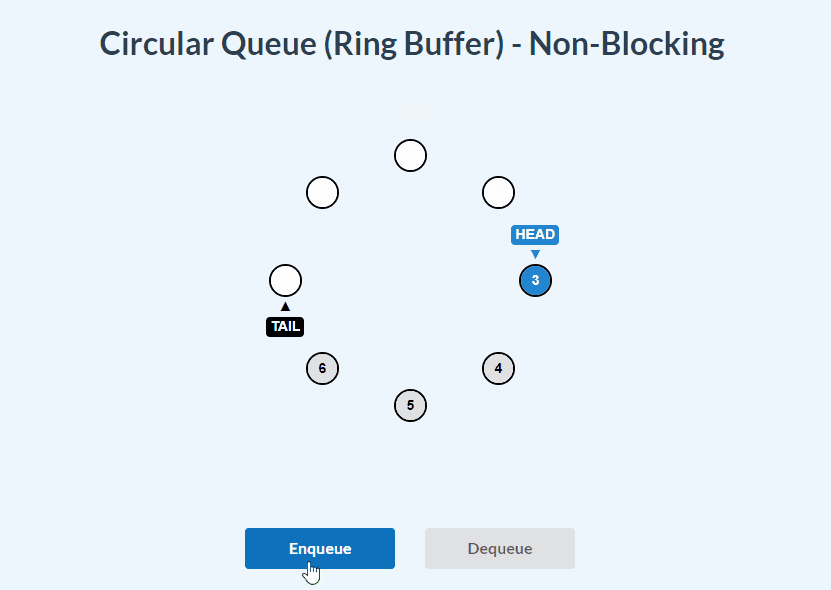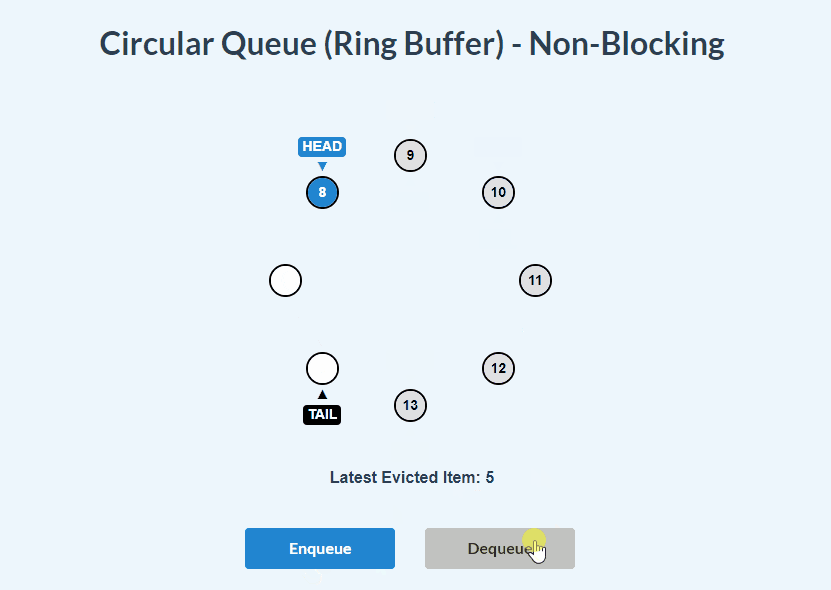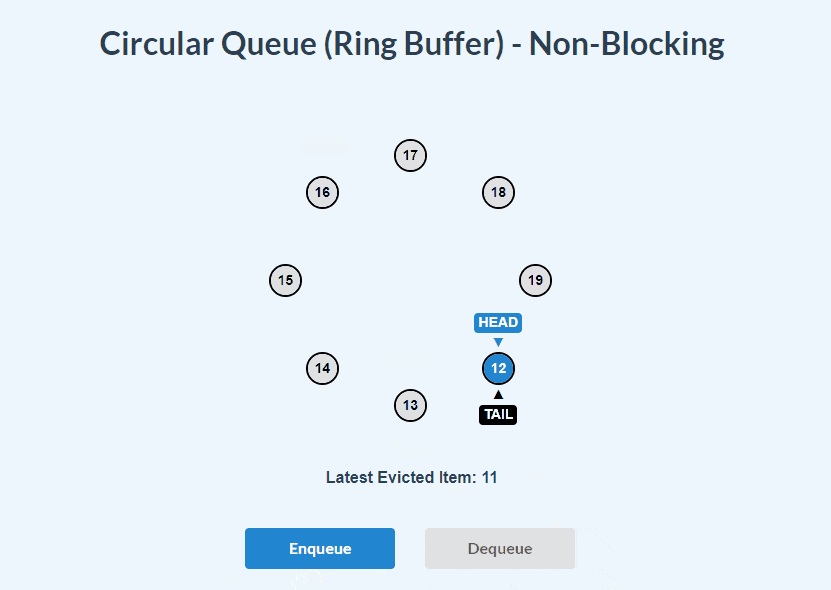
enqueue() and dequeue():

Non-Blocking Circular Queue implementation:

class CircularQueueNonBlocking {
  constructor(capacity, evictionCallback) {
    // Validate capacity
    if (typeof capacity !== 'number' || capacity < 1) {
      throw new Error('Please specify capacity of the Queue')
    }

    // Validate optional eviction callback function
    if (!!evictionCallback && typeof evictionCallback !== 'function') {
      throw new Error('evictionCallback should be a function')
    }

    this.head = 0
    this.tail = 0
    this.size = 0
    this.items = Array.from({ length: capacity })
    this.capacity = capacity
    this.evictionCallback = evictionCallback || null
  }

  enqueue(item) {
    if (this.isFull()) {
      // if it is full, use _rotateHead method to remove the current head value
      // and move the head pointer one step forward:
      const removedItem = this._rotateHead()
      // pass the removedItem into evictionCallback if it is present:
      if (this.evictionCallback) {
        this.evictionCallback(removedItem)
      }

      // add the new item:
      this.items[this.tail] = item
      
      // move the tail one step forward for next insertion in advance:
      this.tail = (this.tail + 1) % this.capacity
    } else {
      // if it is not full, attach the item to current tail, then move the tail one step forward:
      this.items[this.tail] = item
      this.tail = (this.tail + 1) % this.capacity
      this.size++
    }
  }

  dequeue() {
    if (this.isEmpty()) throw new Error('Queue is empty!')

    // store the item about to be removed:
    const removedItem = this.peek()

    // set the current head to be undefined (cleanup)
    this.items[this.head] = undefined

    // move the head index by 1 using modulus operator:
    this.head = (this.head + 1) % this.capacity
    this.size--
    return removedItem
  }
  
  peek() {
    return this.items[this.head]
  }
  
    // helper method for overwriting the oldest item in the queue
  _rotateHead() {
    // store the item that is about to be evicted from queue:
    const removedItem = this.peek()
    // move the head to the next position (next oldest item in the list) using modulus logic
    this.head = (this.head + 1) % this.capacity
    // return the removedItem:
    return removedItem
  }

  isFull() {
    return this.capacity === this.size
  }

  isEmpty() {
    return this.size === 0
  }
  
  length() {
    return this.size
  }
  
  clear() {
    this.items = []
    this.head = 0
    this.tail = 0
    this.size = 0
  }
  
  toArray() {
    return this.items
  }
}