Graphs are powerful data structures that excel at representing relationships and connections between objects. In the real world, graphs can model diverse scenarios such as social networks, transportation systems, computer networks, and even recommendations on e-commerce sites.
These non-linear and non-hierarchical structures consist of vertices (or nodes) and edges that create the links between them. Vertices can represent entities like individuals, locations, or objects, and the edges map the relationships or interactions between them.
While graphs share the non-linear quality with trees, they are distinct in their lack of hierarchical structure; in other words, graphs do not revolve around a central root node. This similarity is not superficial, as trees are actually a special category of graphs (Directed Acyclic Graphs). We will take a look at different type of graphs in more detail in the further sections.
The tone of this article is assuming you are at least familiar with the Tree data structure. If you need a quick refresher, I’d suggest you to start from “Introduction to Trees” article below, then come back and continue here later:
Deep Dive into Data structures using Javascript - Introduction to Trees
This article is intended to be a comprehensive introduction guide for Graphs, as a result it is quite lengthy. If you’re looking for a specific section, feel free to use the table of contents below to directly navigate to the part you are interested.
Table of Contents
Anatomy of a Graph
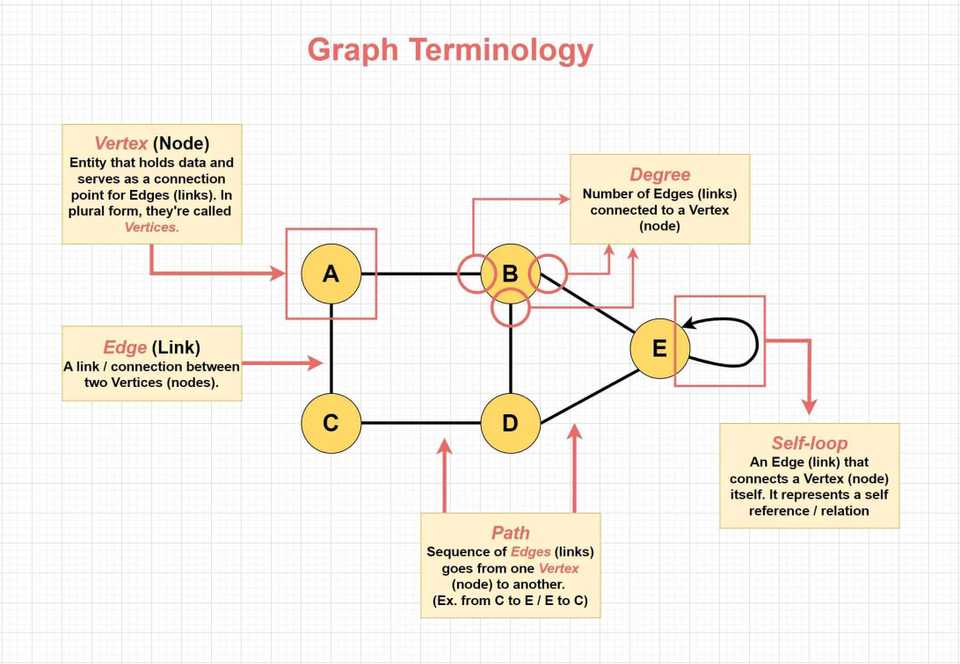
Graphs has a complex and advanced anatomy that can be intimidating especially for those new to the subject. Before diving deeper into the types and inner workings of Graphs, let’s start with getting familiar with the common terminologies:
Graph Terminologies:
- Vertices (Nodes): These are the fundamental units of a graph, representing the entities or objects being modeled.
- Edges (Links): Edges are the connections between vertices, representing the relationships or associations between entities.
- Adjacent (Neighbor): In a graph, two vertices (nodes) are considered adjacent if they are directly connected by an edge, indicating an immediate relationship or link between them.
- Degree: The degree of a vertex is the number of edges connected to it. In a directed graph, vertices have an in-degree (number of incoming edges) and an out-degree (number of outgoing edges).
- Path: A path is a sequence of vertices connected by edges, allowing you to traverse from one vertex to another.
- Self-loop: A self-loop is an edge that connects a vertex to itself. This represents a scenario where an entity is associated with or relates back to itself within the graph’s context.
- Cycle: A cycle is a path that starts and ends at the same vertex, forming a closed loop.
Types of Graph data structure
Graph is a broad term that includes variety of implementations that are designed to solve specific problems. “Type of graph” refers to the distinctive characteristics and configurations that define how the graph operates and what it can represent. A graph type can be on its own, or based on your use case it could also be a composition of types, such as a Directed Acyclic Graph (DAG) or an Undirected Weighted Graph, etc.
We’ll be looking at most commonly used type of Graphs in this section one at a time. Once again it’s important to understand that these types are not mutually exclusive; they can be combined to create more specialized graph structures tailored to specific requirements. For example, a graph can be both directed and weighted, or acyclic and unweighted, depending on the problem at hand.
Directed and Undirected Graphs
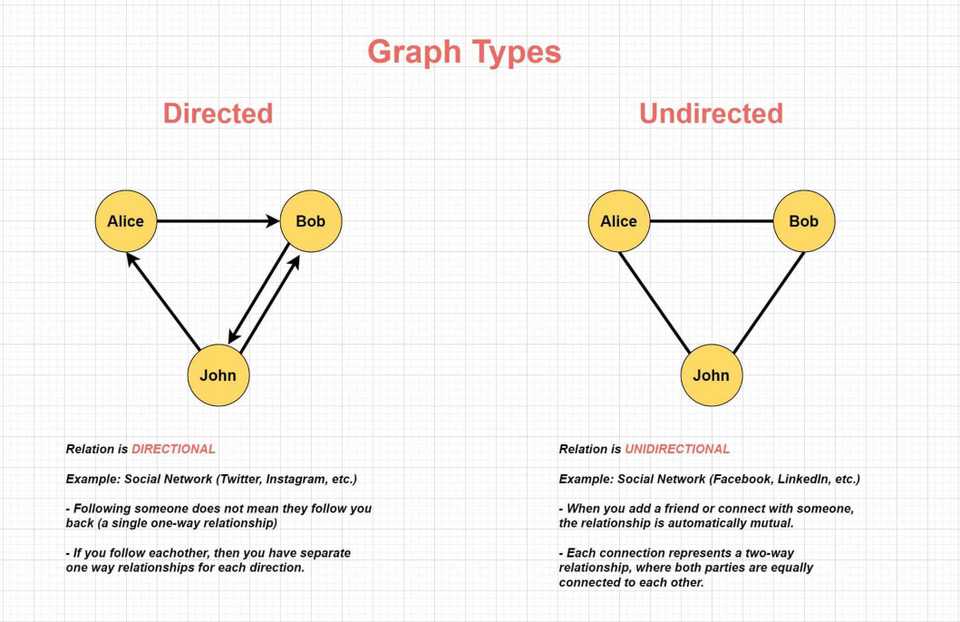
Directed Graph
In a directed graph, the relationships between vertices (nodes) are directional, meaning they flow in a specific direction. This is useful for representing scenarios where the connection or relationship is not mutual or reciprocal. For instance, in social networks like Twitter or Instagram, when you follow someone, it does not automatically mean they follow you back. Each follow represents a single one-way relationship. Even if two users follow each other, there are two separate one-way relationships, one in each direction.
Undirected Graph
In contrast to directed graph, undirected graphs represent relationships that are bidirectional or mutual. When you establish a connection between two vertices, it automatically implies a two-way relationship, meaning both vertices are connected to each other. This is useful for modeling scenarios like friendships on social networks like Facebook or LinkedIn, where adding someone as a friend or connection creates a mutual relationship.
Weighted and Unweighted Graphs
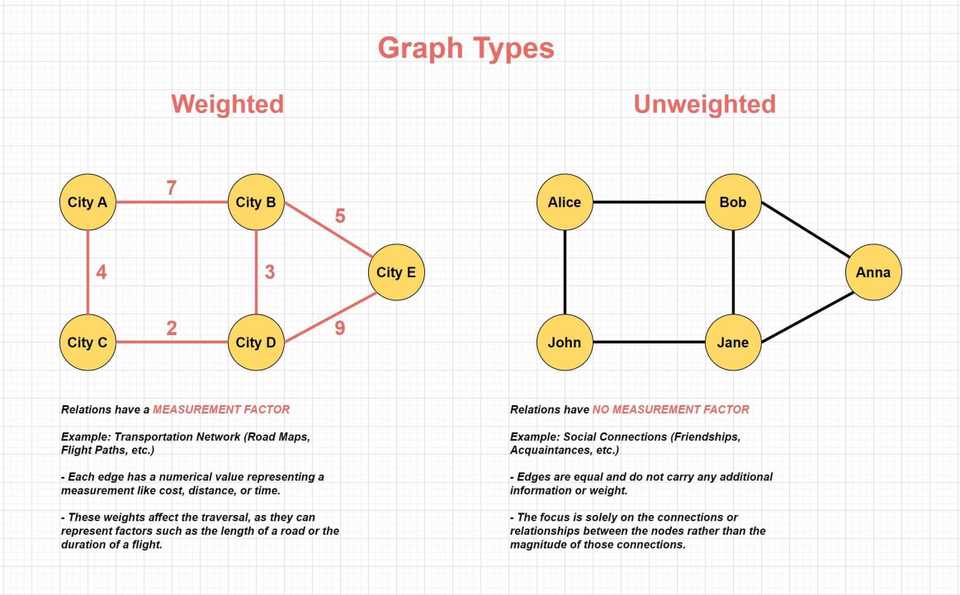
Weighted Graph
In a weighted graph, each edge (connection between vertices) has an associated numerical value, called a weight. These weights can represent measurements or costs related to the relationship, such as the distance between two cities in a road network or the duration of a flight between two airports. The weights play a crucial role in various graph algorithms, as they affect the traversal and decision-making processes based on factors like the length of a path or the total cost involved.
An edge in a weighted graph typically has a numerical weight assigned to represent the cost, capacity, or strength of the connection. If no specific weight is assigned, a default value, often 1 or 0, may be used depending on the application’s requirements or the context of the graph.
Unweighted Graph
Unweighted graphs on the other hand, do not have any numerical values associated with their edges. All connections are treated equally, without any additional measurements or costs. This type of graph is useful for modeling scenarios where the primary concern is the existence of relationships or connections between vertices, rather than any quantitative aspects of those connections. Social networks, where the focus is on the relationships themselves (e.g., friendships or acquaintances), are a common example of unweighted graphs.
Cyclic and Acyclic Graphs
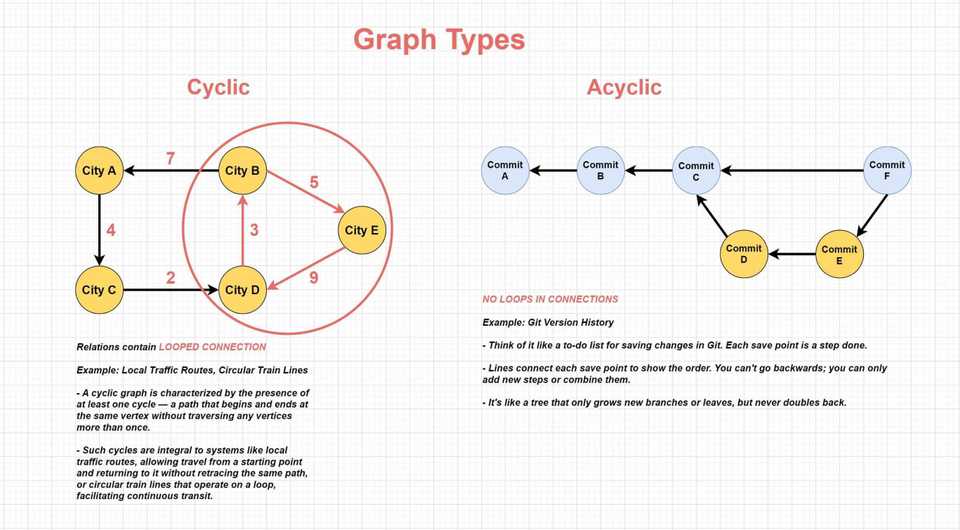
Cyclic Graph
A cyclic graph is one that contains at least one cycle, which is a path that starts and ends at the same vertex, without revisiting any other vertices more than once. Cycles are essential in certain applications, such as local traffic routes, where you can start from a point, travel through multiple locations, and eventually return to the starting point without retracing the same path. Another example is circular train lines, where trains operate in a continuous loop, facilitating uninterrupted transit.
Acyclic Graph
In contrast, an acyclic graph is one that does not contain any cycles. This means that once you start traversing from a vertex, you cannot return to the same vertex without revisiting another vertex more than once. Acyclic graphs are commonly used to represent hierarchical structures or dependencies, where there is a clear flow or direction without any loops or cycles. A good example is the version history in Git, where each commit or save point represents a step in the process, and you cannot go back to a previous step directly; you can only move forward by adding new commits or merging branches.
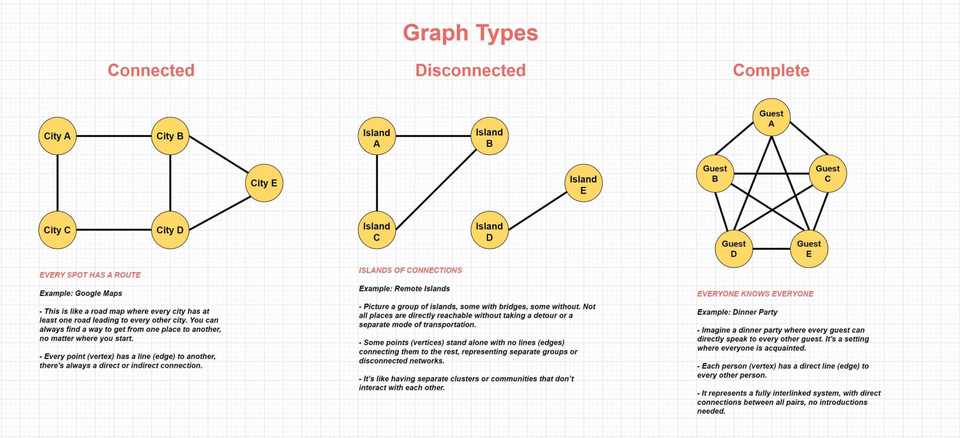
Connected, Disconnected and Complete Graphs
Connected Graph
A connected graph is one where every vertex is reachable from every other vertex through a sequence of edges. In other words, there exists at least one path between any two vertices in the graph. This property is similar to a road map, where you can always find a way to travel from one city to another, either directly or through a series of connected roads.
Disconnected Graph
In contrast, a disconnected graph consists of two or more separate components or subgraphs that are not connected to each other. This means that there are vertices or groups of vertices that have no paths connecting them to other vertices or groups. The analogy of remote islands is fitting, where some islands may have bridges connecting them, while others remain isolated, requiring different modes of transportation to reach them.
Complete Graph
A complete graph is a special type of graph where every vertex is directly connected to every other vertex. This means that for any pair of vertices, there exists an edge connecting them. The analogy of a dinner party where every guest is acquainted with every other guest illustrates this concept well. In a complete graph, there are no introductions needed, as every vertex has a direct connection to all other vertices, representing a fully interlinked system.
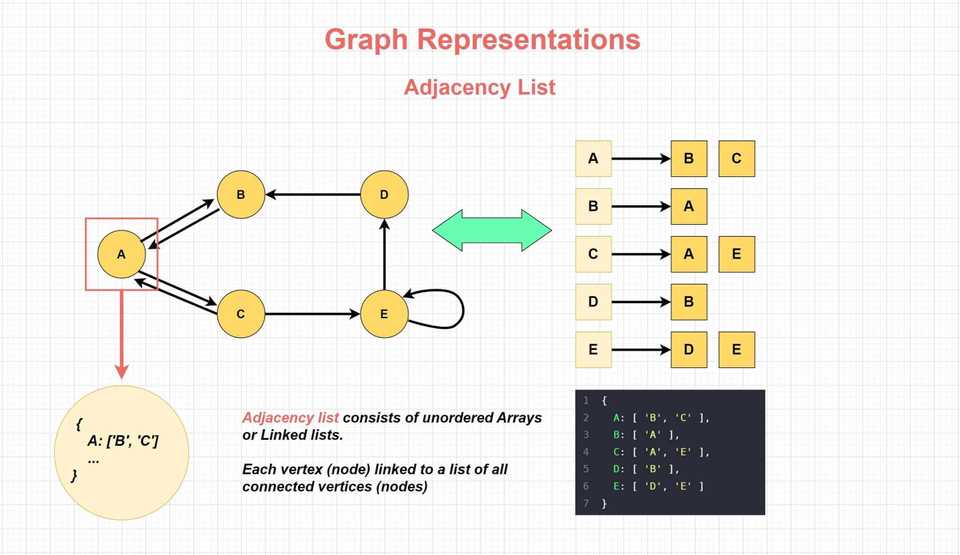
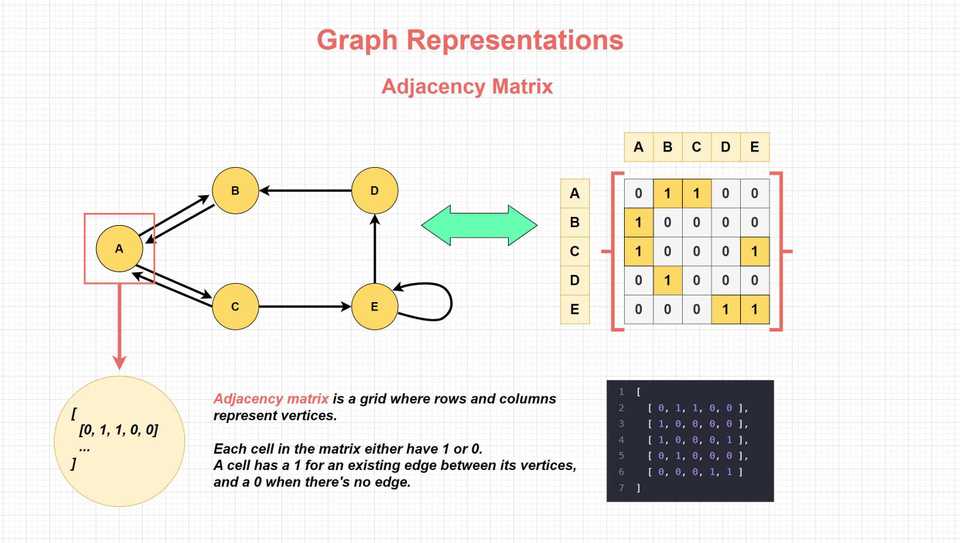
Graph Representations
Graphs can be represented in various ways, and the choice of representation can have a significant impact on the efficiency of graph operations and the memory usage. Two of the most common ways to represent graphs are adjacency lists and adjacency matrices.
Adjacency List
Adjacency list consists of unordered Arrays or Linked lists. Each vertex (node) is associated with a list of all connected vertices (nodes).
This representation is efficient for sparse graphs (graphs with relatively few edges compared to the maximum possible edges) because it only stores the existing edges. It is well-suited for operations that involve iterating over the neighbors of a vertex, such as depth-first search (DFS) or breadth-first search (BFS).
Adjacency Matrix
Adjacency matrix is a grid where rows and columns represent vertices:
- Each cell in the matrix either has a 1 or a 0.
- A cell has a 1 for an existing edge between its corresponding vertices, and a 0 when there’s no edge.
This representation is efficient for dense graphs (graphs with many edges) because it provides constant-time access to check if an edge exists between any two vertices. It is well-suited for operations that involve checking the existence of an edge between two vertices.
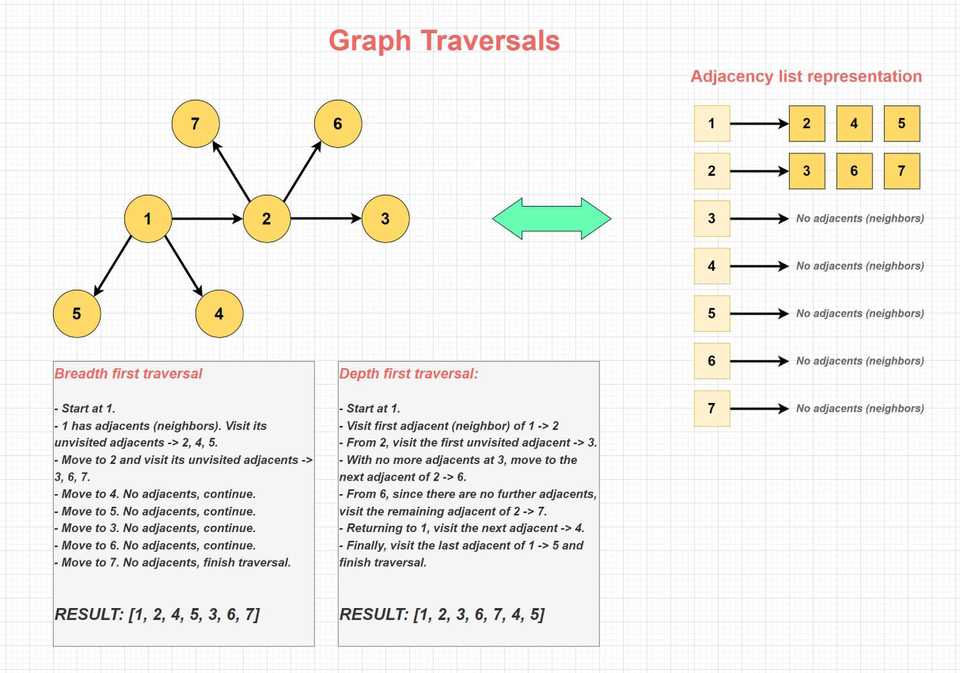
Graph Traversals
Graph traversal algorithms are techniques used to visit and systematically process all the vertices in a graph. These algorithms play a key role in various graph operations, such as finding paths, detecting cycles, and exploring the structure of the graph.
There are different ways to traverse a graph, but we’ll focus on the two most commonly used graph traversal algorithms: Breadth-First Traversal and Depth-First Traversal. If you’re familiar with tree traversals, these names might sound familiar. Although the main mechanism regarding the traversal direction is conceptually similar, they work slightly differently when it comes to graphs.
Unlike tree traversals, where there is a clear hierarchical structure and a defined root node, graph traversals can start from any vertex (node). Additionally, we don’t have subgroups such as pre-order, in-order, or post-order when it comes to depth-first traversals in graphs.
Since we don’t follow a directed traversal like in trees, we must manage the potential cycles to avoid infinite loops during the process. This is typically done by keeping track of visited vertices and avoiding revisiting them.
If you don’t have prior knowledge about tree traversals, it would be beneficial to check out the comprehensive tree traversal guide article below. Understanding tree traversals will provide a solid foundation and make it easier to grasp the concepts of graph traversals:
A Comprehensive Tree Traversal Guide in Javascript - General and Binary Tree Traversals
Breadth First Traversal
The Breadth-First Traversal algorithm explores all the vertices at the current depth level before moving on to vertices at the next depth level. It traverses the graph level by level, starting from a given source vertex. It uses a queue data structure to keep track of the vertices to be visited.
Depth First Traversal
The Depth-First Traversal algorithm explores as far as possible along each branch before backtracking. It visits all the vertices along a path before moving to the next path. It uses a stack data structure to keep track of the vertices to be visited.
When to use Breadth-First vs Depth-First in Graphs?
The choice between Breadth-First and Depth-First depends on the specific problem and the desired behavior. Breadth-First is useful for finding the shortest path between two vertices in an unweighted graph, while Depth-First is useful for topological sorting, detecting cycles, and exploring deeply nested structures.
Once again it’s important to note that graph traversal algorithms must handle cycles to avoid infinite loops. This is typically done by keeping track of visited vertices and avoiding revisiting them. Additionally, traversal algorithms can be modified to accommodate different graph types, such as directed or weighted graphs, by adjusting the traversal rules accordingly.
When to Use a Graph
The decision to use a graph data structure often stems from the need to efficiently model and analyze relationships or connections between entities. Here are some common use cases for graphs:
- Social Networks: Graphs are ideal for representing connections between people in social networks, where vertices represent users, and edges represent relationships or interactions.
- Routing and Navigation Systems: Graphs can model transportation networks, with vertices representing locations (cities, intersections, etc.) and edges representing the routes or paths between them. Weighted edges can represent distances or travel times.
- Recommendation Systems: E-commerce sites and content platforms can use graphs to represent relationships between products, users, and their preferences, enabling personalized recommendations.
- Computer Networks: Graphs can model computer networks, with vertices representing devices (routers, servers, etc.) and edges representing the connections between them.
- Dependency Tracking: In software development, graphs can model dependencies between modules, libraries, or components, helping to analyze and manage complex systems.
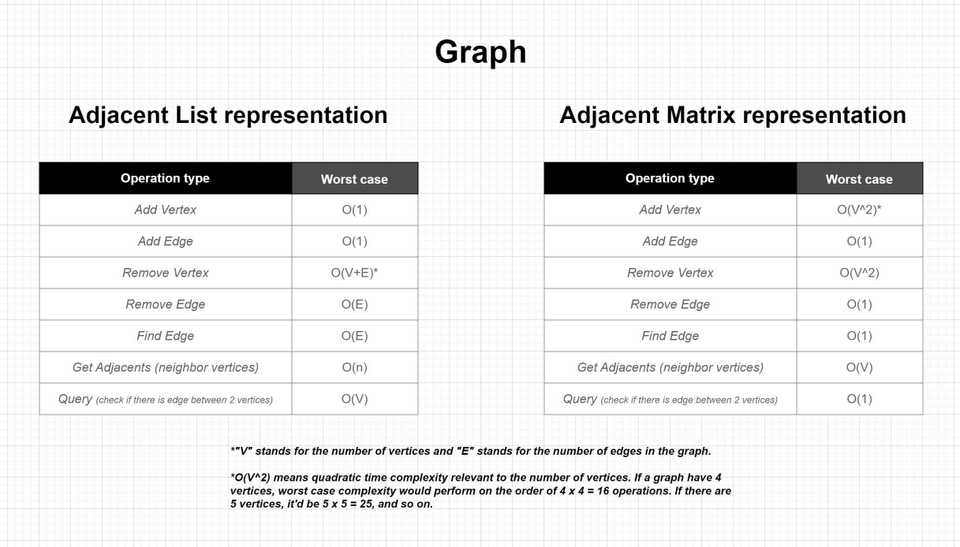
To motivate the choice of using a graph, let’s take a look at the Big O time complexity of common operations:
Here, V represents the number of vertices, and E represents the number of edges.
While adjacency matrices provide constant-time access for querying relationships, they can be inefficient for sparse graphs (graphs with relatively few edges compared to the maximum possible) due to their quadratic space complexity. Adjacency lists often perform better in these cases, with a space complexity proportional to the number of edges.
Graph Implementation in Javascript
To implement a graph in JavaScript, we’ll use an object-oriented approach with a Graph class and a separate Vertex class. I’ll be sharing both adjacency list and adjacency matrix based implementations below. Each variant supports both directed and undirected graphs, as well as weighted and unweighted edges.
Here’s the list of methods in the implementations:
Adjacency List based Graph implementation
Vertex Class:
- constructor(key, value = null): Initializes a new instance of the Vertex class with the provided
keyand optionalvalue. - addEdge(destinationKey, weight = 1): Adds a new edge to the adjacency list of the vertex, with the
destinationKeyand an optionalweight. If no weight is provided, the default value of 1 is used. - removeEdge(destinationKey): Removes an edge from the adjacency list of the vertex by deleting the entry with the given
destinationKey.
Graph Class:
- constructor(directed = true): Initializes a new instance of the Graph class. It takes an optional
directedparameter (default:true) to determine whether the graph should be directed or undirected. - addVertex(key, value = null): Adds a new vertex to the graph with the provided
keyand optionalvalue. If the vertex already exists, it updates the value. - addEdge(sourceKey, destinationKey, weight = 1): Adds an edge between the vertices identified by
sourceKeyanddestinationKey. If the graph is undirected, it adds an edge in both directions. It also supports an optionalweightfor the edge. The default value for an unweighted edge is set to 1. - removeVertex(key): Removes the vertex with the given
keyfrom the graph. It also removes all edges connected to this vertex. - removeEdge(sourceKey, destinationKey): Removes the edge between the vertices identified by
sourceKeyanddestinationKey. If the graph is undirected, it removes the edge in both directions. - breadthFirstSearch(startingVertexKey, targetKey): Performs a breadth-first search (BFS) starting from the vertex identified by
startingVertexKeyto find the vertex with thetargetKey. Returns the target vertex if found, otherwisenull. - depthFirstSearch(startingVertexKey, targetKey): Performs a depth-first search (DFS) starting from the vertex identified by
startingVertexKeyto find the vertex with thetargetKey. Returns the target vertex if found, otherwisenull. - breadthFirstTraversal(startingVertexKey): Performs a breadth-first traversal starting from the vertex identified by
startingVertexKey. Returns an array of vertex keys in the order they were visited. - depthFirstTraversal(startingVertexKey): Performs a depth-first traversal starting from the vertex identified by
startingVertexKey. Returns an array of vertex keys in the order they were visited. - getNeighbors(vertexKey): Returns an array of keys representing the neighboring vertices of the vertex identified by
vertexKey. - printGraph(): Prints the graph representation in an adjacency list format, showing each vertex and its connected edges.
Adjacency Matrix based Graph implementation:
Vertex Class:
- constructor(key, value = null): Initializes a new instance of the Vertex class with the provided
keyand optionalvalue.
Graph Class:
- addVertex(key, value = null): Adds a new vertex to the graph with the provided
keyand optionalvalue. If the vertex already exists, it updates the value. - addEdge(sourceKey, destinationKey, weight = 1): Adds an edge between the vertices identified by
sourceKeyanddestinationKey. If the graph is undirected, it adds an edge in both directions. It also supports optionalweightfor the edge. Unweighted edge default value is set to 1. - removeVertex(key): Removes the vertex with the given
keyfrom the graph. It also removes all edges connected to this vertex. - removeEdge(sourceKey, destinationKey): Removes the edge between the vertices identified by
sourceKeyanddestinationKey. If the graph is undirected, it removes the edge in both directions. - breadthFirstSearch(startingVertexKey, targetKey): Performs a breadth-first search (BFS) starting from the vertex identified by
startingVertexKeyto find the vertex with thetargetKey. Returns the target vertex if found, otherwisenull. - depthFirstSearch(startingVertexKey, targetKey): Performs a depth-first search (DFS) starting from the vertex identified by
startingVertexKeyto find the vertex with thetargetKey. Returns the target vertex if found, otherwisenull. - breadthFirstTraversal(startingVertexKey): Performs a breadth-first traversal starting from the vertex identified by
startingVertexKey. Returns an array of vertex keys in the order they were visited. - depthFirstTraversal(startingVertexKey): Performs a depth-first traversal starting from the vertex identified by
startingVertexKey. Returns an array of vertex keys in the order they were visited. - getNeighbors(vertexKey): Returns an array of keys representing the neighboring vertices of the vertex identified by
vertexKey. - printGraph(): Prints the graph representation in an adjacency matrix format, showing a matrix of edges between vertices.
- _indexToKey(index): A private helper function that converts a vertex index to its corresponding key.
Graphs may seem intimidating, yet they powerfully handle interconnected data and solve complex problems that challenge other data structures. If you want to see how graphs work in an interactive way, I highly recommend playing around with these great graph visualizers at the links below:
- Graph Data Structures Visualizer: https://visualgo.net/en/graphds?slide=1
- Graph Traversal Visualizer: https://visualgo.net/en/dfsbfs?slide=1
I’ve also included line-by-line explanations for each method in the adjacency list and adjacency matrix implementations for you to follow along with what’s happening in the code.
I hope this article helped you understand what graphs are and how they work! Understanding Graphs for the first time is a solid challenge, it will definitely require investing time into experimentation and exploration - so I’d like to encourage you to experiment with the implementations provided below in your favorite code editor.
Thanks for reading!
Adjacency List based Graph implementation
class Vertex {
// Constructor to create a vertex object
constructor(key, value = null) {
this.key = key; // Unique identifier for the vertex
this.value = value; // Optional value held by the vertex
this.edges = new Map(); // Initialize a map to store edges connected to this vertex
}
// Method to add an edge to another vertex with an optional weight
addEdge(destinationKey, weight = 1) {
this.edges.set(destinationKey, weight); // Adds an edge to the destination vertex with the given weight
}
// Method to remove an edge to another vertex
removeEdge(destinationKey) {
this.edges.delete(destinationKey); // Removes the edge to the destination vertex
}
}
class AdjacencyListGraph {
// Constructor to create a graph object
constructor(directed = true) {
this.directed = directed; // Boolean to indicate if the graph is directed
this.vertices = new Map(); // Initialize a map to store vertices by their keys
}
// Method to add a vertex to the graph
addVertex(key, value = null) {
if (!this.vertices.has(key)) {
// Check if the vertex does not already exist
const vertex = new Vertex(key, value); // Create a new vertex instance
this.vertices.set(key, vertex); // Add the vertex to the vertices map
} else {
this.vertices.get(key).value = value; // Update the value of an existing vertex
}
}
// Method to add an edge between two vertices with an optional weight
addEdge(sourceKey, destinationKey, weight = 1) {
if (!this.vertices.has(sourceKey) || !this.vertices.has(destinationKey)) {
throw new Error("Both vertices must exist to add an edge."); // Ensure both vertices exist
}
this.vertices.get(sourceKey).addEdge(destinationKey, weight); // Add the edge from source to destination
if (!this.directed) {
// If the graph is undirected,
this.vertices.get(destinationKey).addEdge(sourceKey, weight); // add a reverse edge as well
}
}
// Method to remove a vertex from the graph
removeVertex(key) {
if (!this.vertices.has(key)) return; // If the vertex does not exist, return
const vertex = this.vertices.get(key); // Get the vertex object
vertex.edges.forEach((_, destKey) => {
// Remove all outgoing edges
this.vertices.get(destKey).removeEdge(key); // Remove reverse edges from connected vertices
});
this.vertices.forEach((v) => v.removeEdge(key)); // Remove this vertex as a destination from other vertices
this.vertices.delete(key); // Remove the vertex from the vertices map
}
// Method to remove an edge between two vertices
removeEdge(sourceKey, destinationKey) {
if (!this.vertices.has(sourceKey) || !this.vertices.has(destinationKey)) {
throw new Error("Both vertices must exist to remove an edge."); // Ensure both vertices exist
}
this.vertices.get(sourceKey).removeEdge(destinationKey); // Remove the edge from source to destination
if (!this.directed) {
this.vertices.get(destinationKey).removeEdge(sourceKey); // If undirected, remove the reverse edge as well
}
}
// Method for breadth-first search starting from a given vertex and aiming to find a specific vertex
breadthFirstSearch(startingVertexKey, targetKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const queue = [startingVertexKey]; // Initialize the queue with the starting vertex
const visited = new Set(); // Set to track visited vertices
while (queue.length > 0) {
const currentKey = queue.shift(); // Dequeue the front vertex
if (currentKey === targetKey) {
return this.vertices.get(currentKey); // If the target is found, return the vertex
}
if (!visited.has(currentKey)) {
visited.add(currentKey); // Mark the current vertex as visited
const neighbors = Array.from(
this.vertices.get(currentKey).edges.keys()
); // Get all neighbors
queue.push(...neighbors.filter((neighbor) => !visited.has(neighbor))); // Enqueue unvisited neighbors
}
}
return null; // Return null if the target is not found
}
// Method for depth-first search starting from a given vertex and aiming to find a specific vertex
depthFirstSearch(startingVertexKey, targetKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const stack = [startingVertexKey]; // Initialize the stack with the starting vertex
const visited = new Set(); // Set to track visited vertices
while (stack.length > 0) {
const currentKey = stack.pop(); // Pop the top vertex from the stack
if (currentKey === targetKey) {
return this.vertices.get(currentKey); // If the target is found, return the vertex
}
if (!visited.has(currentKey)) {
visited.add(currentKey); // Mark the current vertex as visited
const neighbors = Array.from(
this.vertices.get(currentKey).edges.keys()
); // Get all neighbors
stack.push(
...neighbors.filter((neighbor) => !visited.has(neighbor)).reverse()
); // Push unvisited neighbors onto the stack, reversed to maintain order
}
}
return null; // Return null if the target is not found
}
// Method for breadth-first traversal of the graph starting from a given vertex
breadthFirstTraversal(startingVertexKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const queue = [startingVertexKey]; // Initialize the queue with the starting vertex
const visited = new Set(); // Set to track visited vertices
const result = []; // List to store the order of visited vertices
while (queue.length > 0) {
const currentKey = queue.shift(); // Dequeue the front vertex
if (!visited.has(currentKey)) {
visited.add(currentKey); // Mark the current vertex as visited
result.push(currentKey); // Add the vertex to the result list
const neighbors = Array.from(
this.vertices.get(currentKey).edges.keys()
); // Get all neighbors
queue.push(...neighbors.filter((neighbor) => !visited.has(neighbor))); // Enqueue unvisited neighbors
}
}
return result; // Return the list of visited vertices in order
}
// Method for depth-first traversal of the graph starting from a given vertex
depthFirstTraversal(startingVertexKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const stack = [startingVertexKey]; // Initialize the stack with the starting vertex
const visited = new Set(); // Set to track visited vertices
const result = []; // List to store the order of visited vertices
while (stack.length > 0) {
const currentKey = stack.pop(); // Pop the top vertex from the stack
if (!visited.has(currentKey)) {
visited.add(currentKey); // Mark the current vertex as visited
result.push(currentKey); // Add the vertex to the result list
const neighbors = Array.from(
this.vertices.get(currentKey).edges.keys()
); // Get all neighbors
stack.push(
...neighbors.filter((neighbor) => !visited.has(neighbor)).reverse()
); // Push unvisited neighbors onto the stack, reversed to maintain order
}
}
return result; // Return the list of visited vertices in order
}
// Method to get all neighbors of a vertex
getNeighbors(vertexKey) {
if (!this.vertices.has(vertexKey)) {
throw new Error("Vertex does not exist."); // Ensure the vertex exists
}
return Array.from(this.vertices.get(vertexKey).edges.keys()); // Return all neighboring vertex keys
}
// Method to print the entire graph
printGraph() {
this.vertices.forEach((vertex, key) => {
const edges = Array.from(vertex.edges).map(
// Format each edge with its destination and weight
([destinationKey, weight]) => `${destinationKey}(${weight})`
);
// Print each vertex and its connected edges
console.log(`${key} -> ${edges.join(", ")}`);
});
}
}
// Usage example setup code
const graph = new AdjacencyListGraph(); // Directed graph using adjacency list
// Add vertices
graph.addVertex(1);
graph.addVertex(2);
graph.addVertex(3);
graph.addVertex(4);
graph.addVertex(5);
graph.addVertex(6);
graph.addVertex(7);
// Add edges
graph.addEdge(1, 2);
graph.addEdge(1, 4);
graph.addEdge(1, 5);
graph.addEdge(2, 3);
graph.addEdge(2, 6);
graph.addEdge(2, 7);
graph.printGraph();
console.log("BF TRAVERSAL-----------");
graph.breadthFirstTraversal(1);
console.log("DF TRAVERSAL-----------");
graph.depthFirstTraversal(1);
console.log("------------");
graph.breadthFirstSearch(1, 7);
graph.depthFirstSearch(1, 5);
/*
TEST RESULTS:
BFS
Directed - 1, 2, 4, 5, 3, 6, 7
Undirected - 1, 2, 4, 5, 3, 6, 7
DFS
Directed - 1, 2, 3, 6, 7, 4, 5
Undirected - 1, 2, 3, 6, 7, 4, 5
*/Adjacency Matrix based Graph implementation:
class Vertex {
// Constructor to initialize a vertex with a key and an optional value
constructor(key, value = null) {
this.key = key; // Unique identifier for the vertex
this.value = value; // Value associated with the vertex (optional)
}
}
class AdjacencyMatrixGraph {
// Constructor to create a graph object
constructor(directed = true) {
this.directed = directed; // Boolean to indicate if the graph is directed
this.vertices = new Map(); // Map to store vertices with their keys
this.edges = []; // Array to represent the adjacency matrix
}
// Method to add a vertex to the graph
addVertex(key, value = null) {
if (!this.vertices.has(key)) {
// Check if the vertex does not already exist
const vertex = new Vertex(key, value); // Create a new vertex
const index = this.vertices.size; // Determine the next index for the new vertex
this.vertices.set(key, vertex); // Add the vertex to the map
vertex.index = index; // Store the index within the vertex for quick access
this.edges.forEach((row) => row.push(0)); // Extend each existing row in the adjacency matrix with a zero
this.edges.push(new Array(this.vertices.size).fill(0)); // Add a new row for the new vertex
} else {
this.vertices.get(key).value = value; // Update the value of an existing vertex
}
}
// Method to add an edge between two vertices with an optional weight
addEdge(sourceKey, destinationKey, weight = 1) {
if (!this.vertices.has(sourceKey) || !this.vertices.has(destinationKey)) {
throw new Error("Both vertices must exist to add an edge."); // Ensure both vertices exist
}
const sourceIndex = this.vertices.get(sourceKey).index; // Get the matrix index of the source vertex
const destIndex = this.vertices.get(destinationKey).index; // Get the matrix index of the destination vertex
this.edges[sourceIndex][destIndex] = weight; // Set the weight in the adjacency matrix
if (!this.directed) {
// If the graph is undirected,
this.edges[destIndex][sourceIndex] = weight; // set the reciprocal edge as well
}
}
// Method to remove a vertex from the graph
removeVertex(key) {
if (!this.vertices.has(key)) return; // If the vertex does not exist, just return
const index = this.vertices.get(key).index; // Get the matrix index of the vertex
this.edges.splice(index, 1); // Remove the row from the adjacency matrix
this.edges.forEach((row) => row.splice(index, 1)); // Remove the column from the adjacency matrix
this.vertices.delete(key); // Remove the vertex from the map
this.vertices.forEach((v, k) => {
if (v.index > index) {
// Adjust the indices of vertices that followed the removed vertex
v.index--;
}
});
}
// Method to remove an edge between two vertices
removeEdge(sourceKey, destinationKey) {
if (!this.vertices.has(sourceKey) || !this.vertices.has(destinationKey)) {
throw new Error("Both vertices must exist to remove an edge."); // Ensure both vertices exist
}
const sourceIndex = this.vertices.get(sourceKey).index; // Get the matrix index of the source vertex
const destIndex = this.vertices.get(destinationKey).index; // Get the matrix index of the destination vertex
this.edges[sourceIndex][destIndex] = 0; // Set the weight to zero in the adjacency matrix
if (!this.directed) {
this.edges[destIndex][sourceIndex] = 0; // If undirected, also remove the reciprocal edge
}
}
// Method to perform a breadth-first search from a starting vertex to find a target vertex
breadthFirstSearch(startingVertexKey, targetKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const startVertex = this.vertices.get(startingVertexKey); // Get the start vertex
const queue = [startVertex.index]; // Initialize the queue with the index of the start vertex
const visited = new Set(); // Set to track visited vertex indices
while (queue.length > 0) {
const currentIndex = queue.shift(); // Dequeue the first element
const currentKey = this._indexToKey(currentIndex); // Convert index back to vertex key
if (currentKey === targetKey) {
return this.vertices.get(currentKey); // If the target vertex is found, return it
}
if (!visited.has(currentIndex)) {
visited.add(currentIndex); // Mark the current index as visited
this.edges[currentIndex].forEach((weight, index) => {
if (weight > 0 && !visited.has(index)) {
queue.push(index); // Enqueue the index of connected vertices
}
});
}
}
return null; // Return null if the target is not found
}
// Method to perform a depth-first search from a starting vertex to find a target vertex
depthFirstSearch(startingVertexKey, targetKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const startVertex = this.vertices.get(startingVertexKey);
const stack = [startVertex.index]; // Initialize the stack with the index of the start vertex
const visited = new Set(); // Set to track visited vertex indices
while (stack.length > 0) {
const currentIndex = stack.pop(); // Pop the top element
const currentKey = this._indexToKey(currentIndex); // Convert index back to vertex key
if (currentKey === targetKey) {
return this.vertices.get(currentKey); // If the target vertex is found, return it
}
if (!visited.has(currentIndex)) {
visited.add(currentIndex); // Mark the current index as visited
const neighbors = []; // List to hold neighbor indices
this.edges[currentIndex].forEach((weight, index) => {
if (weight > 0 && !visited.has(index)) {
neighbors.push(index); // Collect unvisited connected indices
}
});
neighbors.reverse().forEach((index) => stack.push(index)); // Reverse and push to maintain correct order
}
}
return null; // Return null if the target is not found
}
// Method to perform a breadth-first traversal from a specified starting vertex
breadthFirstTraversal(startingVertexKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const startVertex = this.vertices.get(startingVertexKey); // Get the start vertex
const queue = [startVertex.index]; // Initialize the queue with the index of the start vertex
const visited = new Set(); // Set to track visited vertex indices
const result = []; // List to store the order of visited vertices
while (queue.length > 0) {
const currentIndex = queue.shift(); // Dequeue the first element
const currentKey = this._indexToKey(currentIndex); // Convert index back to vertex key
if (!visited.has(currentIndex)) {
visited.add(currentIndex); // Mark the current index as visited
result.push(currentKey); // Add the current key to result list
this.edges[currentIndex].forEach((weight, index) => {
if (weight > 0 && !visited.has(index)) {
queue.push(index); // Enqueue the index of connected vertices
}
});
}
}
return result; // Return the list of visited vertices in order
}
// Method to perform a depth-first traversal from a specified starting vertex
depthFirstTraversal(startingVertexKey) {
if (!this.vertices.has(startingVertexKey)) {
throw new Error("Starting vertex does not exist."); // Ensure the starting vertex exists
}
const startVertex = this.vertices.get(startingVertexKey);
const stack = [startVertex.index]; // Initialize the stack with the index of the start vertex
const visited = new Set(); // Set to track visited vertex indices
const result = []; // List to store the order of visited vertices
while (stack.length > 0) {
const currentIndex = stack.pop(); // Pop the top element
const currentKey = this._indexToKey(currentIndex); // Convert index back to vertex key
if (!visited.has(currentIndex)) {
visited.add(currentIndex); // Mark the current index as visited
result.push(currentKey); // Add the current key to result list
const neighbors = []; // List to hold neighbor indices
this.edges[currentIndex].forEach((weight, index) => {
if (weight > 0 && !visited.has(index)) {
neighbors.push(index); // Collect unvisited connected indices
}
});
neighbors.reverse().forEach((index) => stack.push(index)); // Reverse and push to maintain correct order
}
}
return result; // Return the list of visited vertices in order
}
// Method to get all neighbors of a specific vertex
getNeighbors(vertexKey) {
if (!this.vertices.has(vertexKey)) {
throw new Error("Vertex does not exist."); // Ensure the vertex exists
}
const index = this.vertices.get(vertexKey).index; // Get the matrix index of the vertex
const neighbors = [];
this.edges[index].forEach((weight, idx) => {
if (weight > 0) {
neighbors.push(this._indexToKey(idx)); // Convert indices to keys and collect as neighbors
}
});
return neighbors; // Return the list of neighbor vertices
}
// Method to print the graph as an adjacency matrix
printGraph() {
const verticesArray = Array.from(this.vertices.keys()); // Extract vertex keys
console.log(" " + verticesArray.join(" ")); // Print header row with vertex keys
this.edges.forEach((row, i) => {
console.log(verticesArray[i] + " " + row.join(" ")); // Print each row of the adjacency matrix
});
}
// Private helper method to convert a matrix index back to a vertex key
_indexToKey(index) {
return Array.from(this.vertices.keys())[index]; // Convert index to key using map keys extraction
}
}
// Usage example setup code
const graph = new AdjacencyMatrixGraph(false); // Undirected graph using adjacency matrix
// Add vertices
graph.addVertex(1);
graph.addVertex(2);
graph.addVertex(3);
graph.addVertex(4);
graph.addVertex(5);
graph.addVertex(6);
graph.addVertex(7);
// Add edges
graph.addEdge(1, 2);
graph.addEdge(1, 4);
graph.addEdge(1, 5);
graph.addEdge(2, 3);
graph.addEdge(2, 6);
graph.addEdge(2, 7);
graph.printGraph();
console.log("BF TRAVERSAL-----------");
graph.breadthFirstTraversal(1);
console.log("DF TRAVERSAL-----------");
graph.depthFirstTraversal(1);
console.log("------------");
graph.breadthFirstSearch(1, 7);
graph.depthFirstSearch(1, 5);
/*
TEST RESULTS:
BFS
Directed - 1, 2, 4, 5, 3, 6, 7
Undirected - 1, 2, 4, 5, 3, 6, 7
DFS
Directed - 1, 2, 3, 6, 7, 4, 5
Undirected - 1, 2, 3, 6, 7, 4, 5
*/