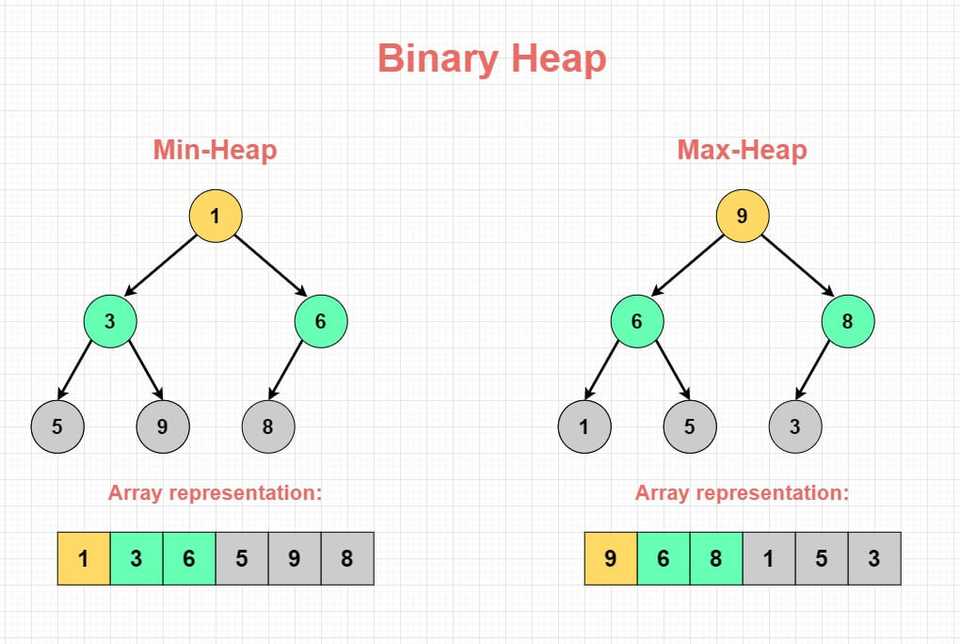
Heap is a fundamental data structure that is constructed as a specialized form of a complete binary tree. They are known to be efficient at organizing data for quick access to the highest or lowest value element based on the “Heap property”.
“Heap property” can be classified into two main types: Max Heaps and Min Heaps. In a Max Heap, each parent node has a value greater than or equal to its child nodes, while in a Min Heap, each parent node has a value less than or equal to its child nodes. Heaps are widely used to create efficient algorithms and support operations for priority queues. They are essential for many applications.
There are various forms of heaps, the most common implementation is the “Binary Heap” - which we will focus on in this article. The tone of this article is assuming you are at least familiar with the concept of Tree data structure and Binary Tree. If that’s not the case or you need a quick refreshment, I’d suggest you start from the “Introduction to Trees” article by following the link below, then come back and continue here later:
Deep dive into data structures using Javascript - Introduction to Trees
Anatomy of a Binary Heap
Heap has an interesting anatomy. It follows the structural design of a complete binary tree - which means that all levels of the tree, except possibly the last, are completely filled, and the nodes in the last level are aligned to the left. The most interesting part is the underlying structure used to achieve this binary tree-like behavior is not a traditional binary tree. Instead, an Array is utilized to represent the Heap to allow efficient access and manipulation of the elements.
Every Heap has two important properties:
Heap Order Property: This property determines the relationship between parent and child nodes. In a Max Heap, parents have values greater than or equal to their children. In a Min Heap, parents have values lesser than or equal to their children.
When it comes to implementations, Min and Max Heaps are nearly identical, except for one key difference: the ‘comparator.’ The comparator is a property that defines the order of the heap. The usual approach is to have a base Heap class, and then extend it by providing a comparator that specifies the desired heap order.
Heap Shape Property: This property guarantees the completeness of the binary tree forming the heap, where all levels, except potentially the last, are fully filled, and the nodes in the last level are arranged in a left-to-right fashion.
In order to maintain these properties and the binary-tree-like behavior, we utilize an array by employing various formulas - such as determining the parent, left, or right child of any element within the Heap.
They play an important role when we maintain the order of the Heap during insertion or deletions. Let’s start with taking a deeper look at how Array representation works in practice.
Array Representation of Binary Heap in Detail
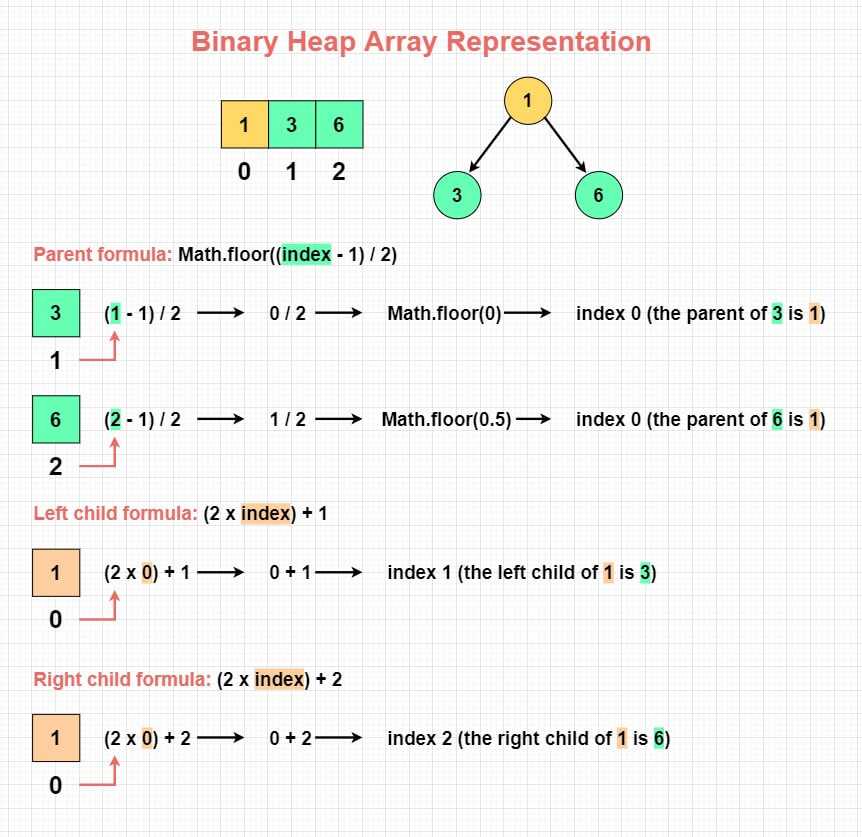
Heap representation in an Array is a popular implementation choice due to its efficient memory usage. In this representation, the positions of the nodes in the heap are mapped to indexes in the array. To figure out the tree-like node positions such as parent, left or right child nodes, we use 3 different formulas:
- Parent: The parent node of a node at index (“i”) can be found at the position determined by (i - 1) / 2 using integer division. In Javascript, this calculation is wrapped with a Math.floor method, such as: Math.floor((i - 1) / 2). The reason we need the floor value of the division is to make sure we get the nearest lower integer value. This is important because array indexes are integer values and cannot have fractional parts.
- Left child: The left children of a node at index (“i”) can be found at positions calculated using the formula 2i+1 or (2 x i) + 1
- Right child: The right children of a node at index (“i”) can be found at positions calculated using the formula 2i+2 or (2 x i) + 2
Take a look at the visual down below to see a basic example of how all these formulas work in practice:
How does Heap order stays maintained
The order of a heap is maintained through a process known as “heapifying”. There are two types of heapify operations: heapifyUp (also known as siftUp or bubbleUp), which is usually performed after an insertion, and heapifyDown (also known as siftDown or bubbleDown), which is generally done after a removal.
Insertion and heapifyUp
When a new element is inserted into a heap, it is initially placed at the next available position in the array representation of the heap (which is the end of the array). But this might violate the heap property as the newly inserted element might be greater (or smaller, in case of a min heap) than its parent.
To restore the heap property, the heapifyUp operation is performed. During heapifyUp, we compare the inserted element with its parent. If the inserted element is smaller than it’s parent in a min heap (or larger in a max heap), then we swap the element with its parent. We continue this process up the heap until the heap property is restored, i.e., each parent node is greater (or smaller, for a min heap) than its child nodes.
In simpler terms:
- We insert the element at the end of the array.
- We bubble up the newly inserted element by starting from the last node.
- We take 2 actions on each step: first we compare a node with it’s parent and swap their values if necessary, then move to the next parent until we reach to the root node.
Take a closer look at the gif below to visualize how heapifyUp works in practice in a Min Heap:
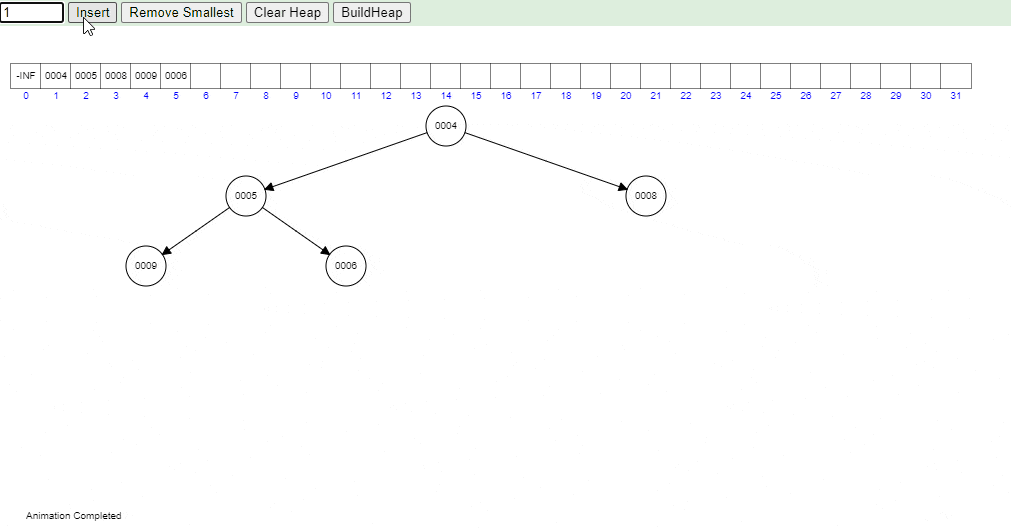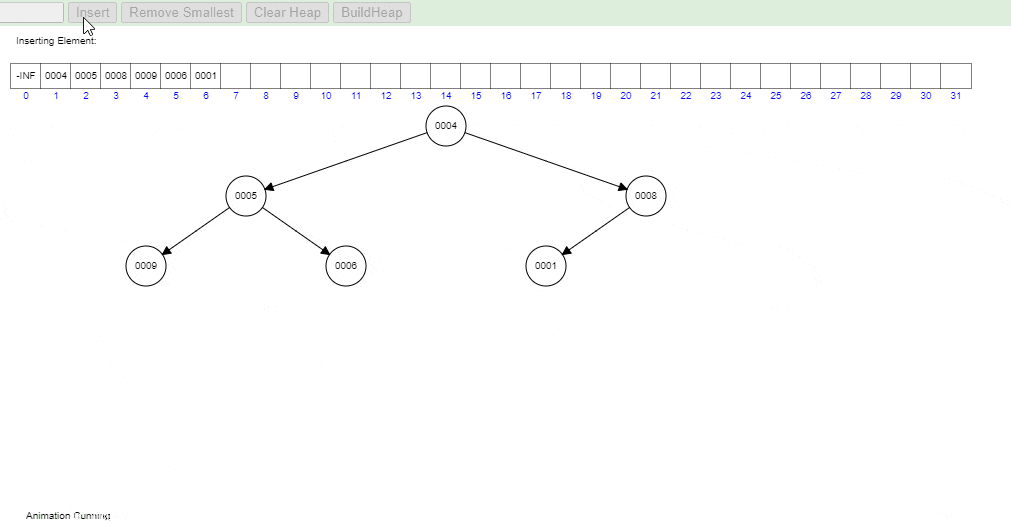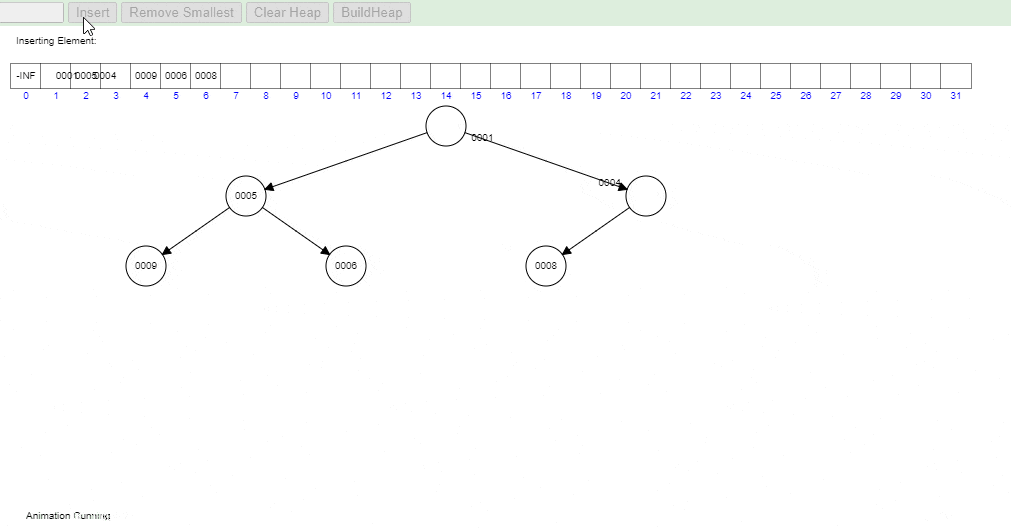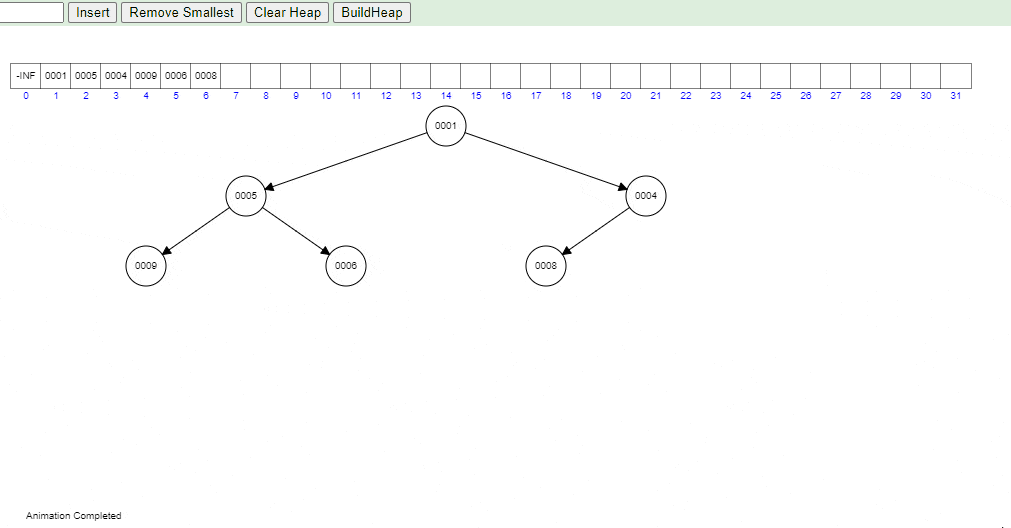
- Visual generated at: https://www.cs.usfca.edu/~galles/visualization/Heap.html
Removal and heapifyDown
When an element is removed from a heap, we typically remove the root element, as this operation can be performed in constant time. But this leaves a hole at the root of the heap. To fill this gap, we move the last element in the heap into the root position. This might violate the heap property, as this element element might be larger (or less, in case of a max heap) than its children.
To restore the heap property, the heapifyDown operation is performed. During heapifyDown, we compare the root element with its children. If the root element is larger than either of its children in a min heap (or smaller in a max heap), we swap the root element with its smaller (or larger, for a max heap) child. We continue this process down the heap until the heap property is restored.
These heapify operations ensure that a heap maintains its order and satisfies the heap property at all times, whether we’re adding new elements or removing existing ones from the heap. By using an array representation and the heapifyUp and heapifyDown operations, we can guarantee that the heap remains balanced, making operations like insertions, deletions, and finding the min/max element highly efficient.
Take a closer look at the gif below to visualize how heapifyDown works in practice in a Min Heap:
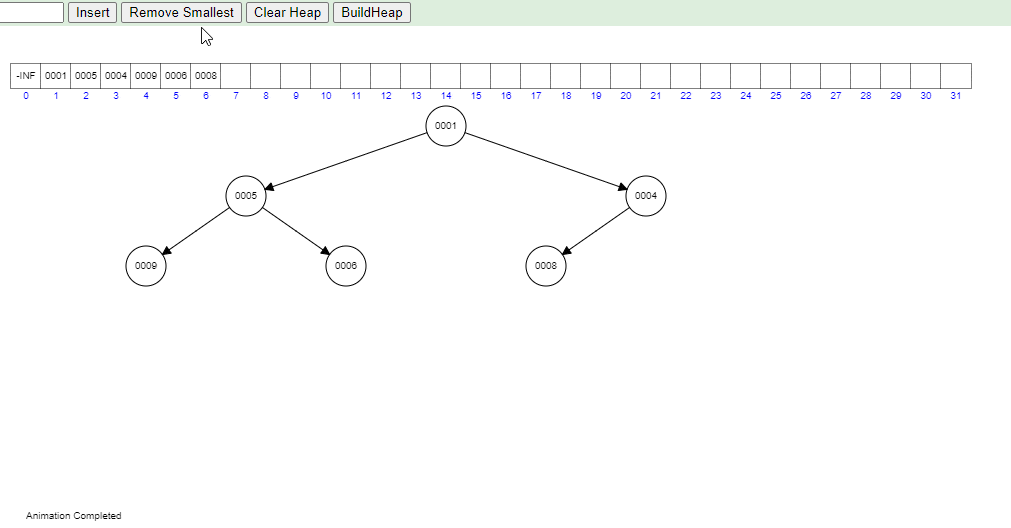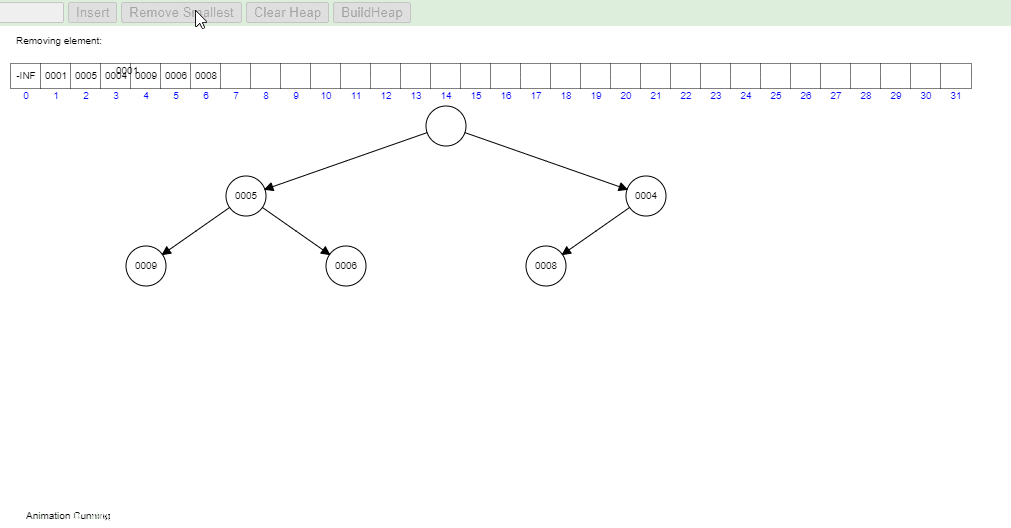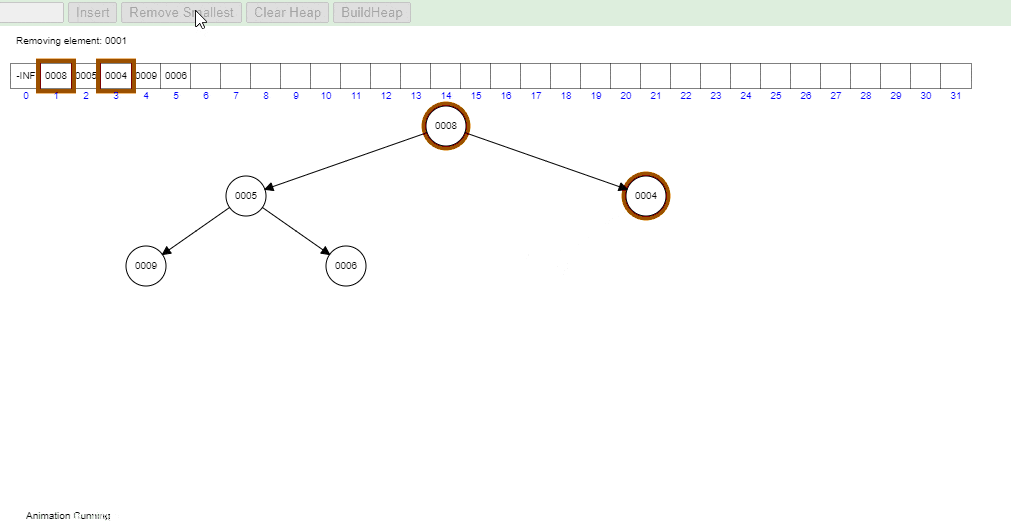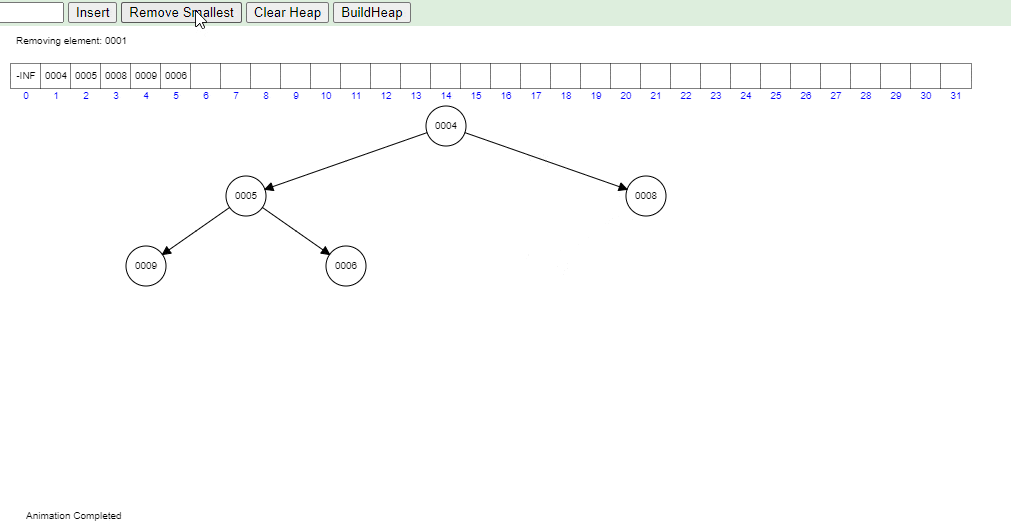
- Visual generated at: https://www.cs.usfca.edu/~galles/visualization/Heap.html
When to use Heap
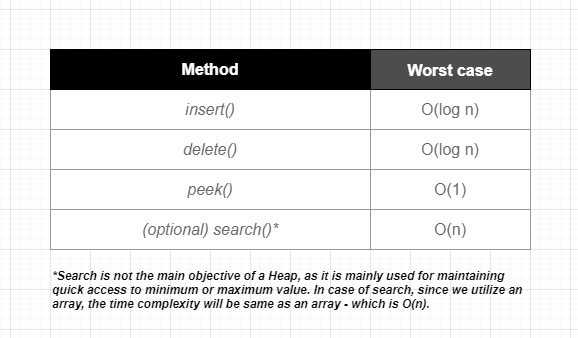
Heaps have unique properties that make them useful in specific situations. Let’s start with taking a look at the Big O of common operations in Heap:
Insertion Operation (Insert): It takes O(log n) time complexity. In the worst case, we may have to go up to the root (the height of the heap) while inserting.
Deletion Operation (Delete): It also takes O(log n) time complexity. Removing a node could require traversing the heap from the root to the leaf node.
Getting Minimum/Maximum (Peek): It takes O(1) time complexity. The minimum or maximum element (depending on the heap type) is always at the root.
Search (optional): Search is not the main objective of a Heap, as it is mainly used for maintaining quick access to minimum or maximum value. In case of search, since we utilize an array, the time complexity will be same as array - which is O(n)
Considering these time complexity analyses, heaps are incredibly useful in the following situations:
Priority Queues: Heaps are the preferred data structure for implementing priority queues. A priority queue is a special type of queue where each element has a priority and is served according to that priority.
Heap Sort: Heapsort is a sorting algorithm that uses a binary heap data structure. It has a time complexity of O(n log n), which makes it efficient for large datasets.
Graph Algorithms: Heaps are widely used in graph algorithms like Dijkstra’s algorithm and Prim’s algorithm. These algorithms require a data structure that can quickly provide the minimum or maximum element, which heaps handle efficiently.
K’th Largest/Smallest Element: Heaps can efficiently solve problems related to finding the k’th smallest or largest element in an array. This involves building a min heap or max heap and performing remove operations k times.
Sliding Window Problems: Heaps are helpful in problems where you need to find the maximum/minimum element in a sliding window. They can perform insertions and deletions in logarithmic time.
Heap implementation in Javascript
We will be using ES6 Classes to build our Heap. The MinHeap and MaxHeap subclasses are also included - they inherit from the Heap class. MinHeap uses a comparator that sorts the heap in ascending order, while MaxHeap uses a comparator that sorts the heap in descending order.
Here is the list of methods we are going to implement:
size(): Returns the number of items in the heap.isEmpty(): Checks if the heap is empty.peek(): Returns the top element (minimum or maximum value) in the heap without removing it.insert(value): Adds a new value to the heap and maintains the heap property. It’s a fundamental operation for adding elements to the heap.delete(): Removes and returns the top element (minimum or maximum value) in the heap while maintaining the heap property. It’s a fundamental operation for removing elements from the heap.parentIndex(i),parentValue(i),leftChildIndex(i),leftChildValue(i),hasLeftChild(i),rightChildIndex(i),rightChildValue(i),hasRightChild(i): Helper methods for navigating the heap structure. They are relevant for calculating indexes and accessing parent and child node indexes or values.heapifyUp(): Rearranges the heap after adding a new element. It ensures the heap property is maintained and is relevant to the insertion process.heapifyDown(): Moves a node down the heap until it’s in the correct position. It ensures the heap property is maintained and is relevant to the deletion process.displayHeap(heap): Displays the heap as a binary tree in level-order. It’s useful for visualization and debugging purposes.
Heaps are not the most advanced data structures, but they can be still tricky to understand at the beginning. My suggestion would be first getting familiar with its array representation of a binary tree - which includes how to find parent, left or right child of any element by using the array index formulas. Then taking a closer look at the mechanics of how does insert and delete utilizes heapifyUp and heapifyDown methods.
If you want to see how Heap operations work in a practical way, I highly recommend playing around with this great Heap visualizer at the link below:
https://www.cs.usfca.edu/~galles/visualization/Heap.html
Additionally, I’ve also included line-by-line explanations for each method in the implementation for you to follow up what is happening in the code. I hope this article helped you to understand what Heaps are and how they work! I’d like to encourage you to experiment with the implementation below in your favorite code editor. Thanks for reading!
Implementation of Heap in Javascript
class Heap {
// The constructor method is called when a new instance of Heap is created.
constructor(comparator) {
// Initialize the heap array.
this.heap = [];
// Set the comparator method for comparing nodes in the heap.
// If no comparator function is provided, it defaults to a comparison
// function that sorts in ascending order (a min-heap).
this.comparator = comparator || ((a, b) => a - b);
}
// Return the number of items in the heap.
size() {
return this.heap.length;
}
// Check if the heap is empty.
isEmpty() {
return this.size() == 0;
}
// Get the top element in the heap without removing it.
// For a min-heap, this will be the smallest element;
// for a max-heap, it will be the largest.
peek() {
return this.heap[0];
}
// Add a new value to the heap.
insert(value) {
// First, add the new value to the end of the array.
this.heap.push(value);
// Then, move the new value up the heap to its correct position.
this.heapifyUp();
}
// Remove and return the top element in the heap.
delete() {
// If the heap is empty, just return null
if (this.isEmpty()) {
return null;
}
// Save the top element so we can return it later.
const poppedValue = this.peek();
// If there is more than one node in the heap, move the last node to the top.
const bottom = this.size() - 1;
if (bottom > 0) {
this.swap(0, bottom);
}
// Remove the last node (which is now the top node) from the heap.
this.heap.pop();
// Move the new top node down the heap to its correct position.
this.heapifyDown();
// Finally, return the original top element.
return poppedValue;
}
// Method to get the index of a node's parent.
parentIndex(i) {
/*
About Math.floor:
We take the floor value of the division to
make sure we get the nearest lower integer value.
This is important because array indexes
are integer values and cannot have fractional parts.
*/
return Math.floor((i - 1) / 2);
}
// Method to get the value of a node's parent.
parentValue(i) {
/*
Check if the index is within the bounds of the heap and the parent exists.
If the index is less than the heap's size and the parent index is greater than or equal to 0, it means the parent exists.
If it doesn't exist or the index is out of bounds, we return undefined.
*/
return i < this.size() && this.parentIndex(i) >= 0
? this.heap[this.parentIndex(i)]
: undefined;
}
// Method to get the index of a node's left child.
leftChildIndex(i) {
return 2 * i + 1;
}
// Method to get the value of a node's left child.
leftChildValue(i) {
/*
Check if the left child exists.
If the left child index is less than the size of the heap, it means the left child exists.
If it doesn't exist, we return undefined.
*/
return this.hasLeftChild(i) ? this.heap[this.leftChildIndex(i)] : undefined;
}
// Method to check if a node has left child.
// It returns true if the left child index is within the valid range of heap indexes,
// which indicates that a left child exists.
hasLeftChild(i) {
return this.leftChildIndex(i) < this.size();
}
// Method to get the index of a node's right child.
rightChildIndex(i) {
return 2 * i + 2;
}
// Method to get the value of a node's right child.
rightChildValue(i) {
/*
Check if the right child exists.
If the right child index is less than the size of the heap, it means the right child exists.
If it doesn't exist, we return undefined.
*/
return this.hasRightChild(i)
? this.heap[this.rightChildIndex(i)]
: undefined;
}
// Method to check if a node has right child.
// It returns true if the right child index is within the valid range of heap indexes,
// which indicates that a right child exists.
hasRightChild(i) {
return this.rightChildIndex(i) < this.size();
}
// Method to swap the values of two nodes in the heap.
swap(i, j) {
// Swap the values of elements at indices i and j without using a temporary variable:
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
}
// This method is used to rearrange the heap after adding a new element.
heapifyUp() {
// We start from the last node in the heap. This is the node that was most recently added.
let nodeIndex = this.size() - 1;
/*
In the while loop, we swap the values to maintain the heap property.
When? If the following 2 conditions are true:
- "nodeIndex > 0":
This means we haven't reached to the main parent yet.
- "this.comparator(parentNodeValue, currentNodeValue) > 0":
If this is true, it means the heap property is violated and we need to swap values.
"comparator" function here compares if the current node is smaller or bigger than it's parent.
Based on the heap order, comparator function will be slightly different. Such as:
((a, b) => (a - b) for min heap
((a, b) => (b - a) for max heap
*/
while (
// The node is not the root (it has a parent).
nodeIndex > 0 &&
this.comparator(this.parentValue(nodeIndex), this.heap[nodeIndex]) > 0
) {
// The heap property is violated for our node and its parent. We need to swap them to restore the heap property.
this.swap(nodeIndex, this.parentIndex(nodeIndex));
// After swapping, our node has moved one level up the heap. We update nodeIndex to the index of the parent.
// In the next iteration of the loop, we'll check the heap property for the node and its new parent.
nodeIndex = this.parentIndex(nodeIndex);
}
}
// Method to move a node down the heap until it is in the correct position.
// Used after a deletion
heapifyDown() {
// We start from the top node in the heap which is the root, always at index 0.
// So we initialize the current node index at 0.
let currNodeIndex = 0;
// The 'while' loop continues as long as the current node has a left child.
// The reason for this is that a heap is a complete binary tree and hence,
// a node would have a left child before it has a right child.
while (this.hasLeftChild(currNodeIndex)) {
// Assume the smaller child is the left one.
let smallerChildIndex = this.leftChildIndex(currNodeIndex);
/*
Check if there's a right child and compare it to the left child.
If the right child is smaller, update the smallerChildIndex to the right child's index
Based on the heap order, comparator function will be slightly different. Such as:
((a, b) => (a - b) for min heap
((a, b) => (b - a) for max heap
*/
if (
this.hasRightChild(currNodeIndex) &&
this.comparator(
this.rightChildValue(currNodeIndex),
this.leftChildValue(currNodeIndex)
) < 0
) {
smallerChildIndex = this.rightChildIndex(currNodeIndex);
}
// If the current node is smaller or equal to its smaller child, then it's already in correct place.
// This means the heap property is maintained, so we break the loop.
if (
this.comparator(
this.heap[currNodeIndex],
this.heap[smallerChildIndex]
) <= 0
) {
break;
}
// If the current node is not in its correct place (i.e., it's larger than its smaller child),
// then we swap the current node and its smaller child.
this.swap(currNodeIndex, smallerChildIndex);
// After swapping, the current node moves down to the position of its smaller child.
// Update the current node index to the smaller child's index for the next iteration of the loop.
currNodeIndex = smallerChildIndex;
}
}
// Displays an array that will represent the heap as a binary tree
// in level-order, with each sub-array representing a level of the tree.
// such as: [ [ 1 ], [ 5, 3 ], [ 9, 6, 8 ] ]
displayHeap() {
let result = [];
let levelCount = 1; // Counter for how many elements should be on the current level.
let currentLevel = []; // Temporary storage for elements on the current level.
for (let i = 0; i < this.size(); i++) {
currentLevel.push(this.heap[i]);
// If the current level is full (based on levelCount), add it to the result and reset currentLevel.
if (currentLevel.length === levelCount) {
result.push(currentLevel);
currentLevel = [];
levelCount *= 2; // The number of elements on each level doubles as we move down the tree.
}
}
// If there are any elements remaining in currentLevel after exiting the loop, add them to the result.
if (currentLevel.length > 0) {
result.push(currentLevel);
}
return result;
}
}
class MinHeap extends Heap {
constructor() {
super((a, b) => a - b); // MinHeap uses a comparator that sorts in ascending order
}
}
class MaxHeap extends Heap {
constructor() {
super((a, b) => b - a); // MaxHeap uses a comparator that sorts in descending order
}
}