Priority Queue is a versatile and efficient data structure, that represents sophisticated and practical approach to data processing. By design, elements are managed not just by the order of their arrival but according to their priority. This mechanism plays an important role in optimizing tasks in numerous applications, from algorithm design to system resource management.
While Priority Queues can be implemented with various data structures like Arrays, Linked Lists, Heaps or Binary Trees - using a Binary Heap is the most popular choice and that’s the implementation we will be focusing on through this article.
Binary Heaps, a common implementation of Heaps, lay the groundwork for Priority Queues. They come in two main types: Max Heaps and Min Heaps. Max Heaps places greater values to be processed first, while the Min Heaps does the opposite - lesser values are favored to be processed first. For Priority Queues, although both types are applicable, the Min Heap version is often favored due to its effectiveness in sorting elements where lower values signify higher priority. I will be sharing an implementation that covers both cases at the end of this article.
In order to fully understand Priority Queues, a solid understanding of Heaps is essential. Therefore the tone of this article is assuming you are familiar with the concept of Heaps. If that’s not the case or you need a quick refreshment, I’d suggest you start from the “Heap” article by following the link below, then come back and continue here later:
Deep dive into data structures using Javascript - Heap
Anatomy of a Priority Queue
Priority Queue format we are discussing here is built on top of Binary Heap, therefore the anatomy is almost identical - except one distinct aspect: the utilization of a “priority” property for each element.
This is the feature where Priority Queue differs from a standard Heap. In a Min or Max heap, the placement mechanism works based on given value, while in the Priority Queue it is based on given priority. The underlying architecture of a Priority Queue is typically an array, mirroring the array representation of a Heap. In this array, each index doesn’t just hold a value but an object or a pair containing the value and its priority.
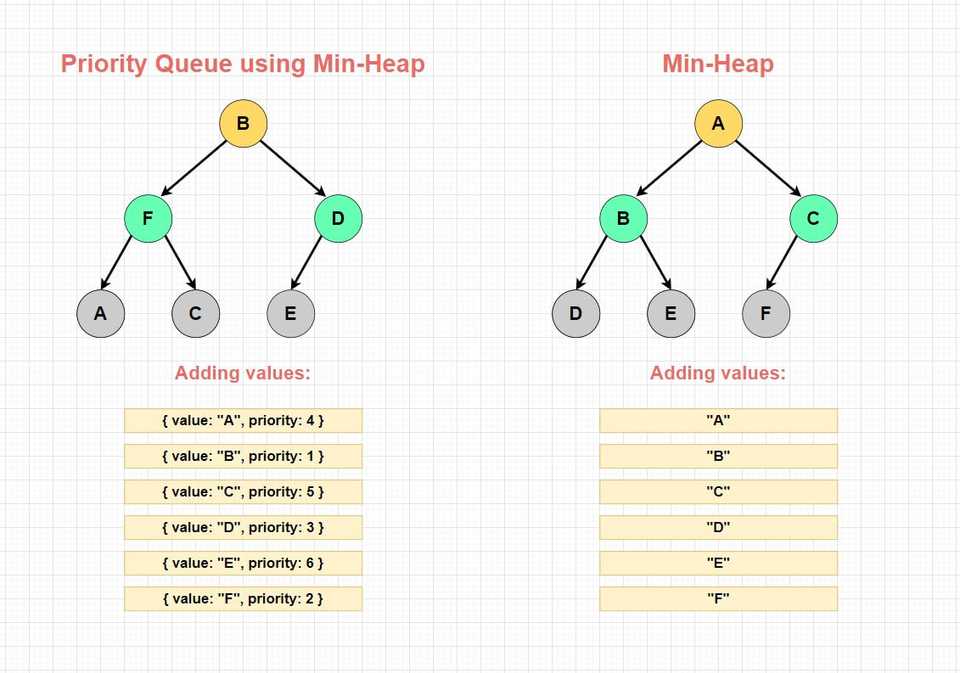
Take a look at the visual below to see the distinction between a Priority Queue using a Min Heap as underlying structure versus a regular Min Heap. Both are shown with their Binary Heap representation, we add the same values following the same order. But there is a small twist - each element added to the Priority Queue has different priorities assigned to them:
When to Use a Priority Queue
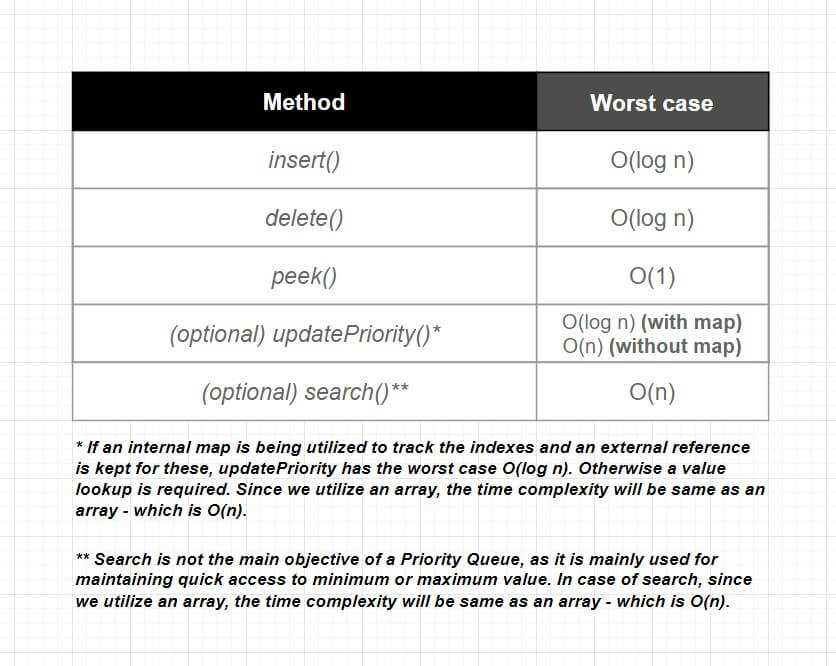
Priority Queues are mostly suited for particular scenarios where the order of item processing is important. Let’s start with taking a look at the Big O of common operations:
Insertion Operation (Enqueue): The insertion of an element, which involves adding a value with a given priority, typically requires O(log n) time complexity. The newly added element may need to ascend towards the front of the queue, especially if it has a high priority, respecting the queue’s ordering rules.
Removal Operation (Dequeue): Removing the element with the highest priority, which is generally at the front of the queue, also takes O(log n) time complexity. This operation may trigger a reorganization of the queue to ensure the next highest priority element comes to the forefront.
Peek Operation: Accessing the element with the highest priority is a constant time operation, O(1), since it is always at the front of the queue, ready to be processed next.
Update Priority Operation (optional): Updating the priority of an element in the Priority Queue can vary in time complexity depending on the underlying implementation.
- With a map: If an internal map is utilized to track the indices and an external reference (ID) is kept for each element, the
updatePriorityoperation can be performed in O(log n) time complexity. This is because the map allows us to directly access the element in the heap, and the only remaining operation is the reorganization of the heap (heapify), which takes O(log n). - Without a map: In the absence of such a map, updating the priority requires a linear search to find the element, resulting in O(n) time complexity. After finding the element, we would still need to perform the heap reorganization, but the dominant factor is the linear search time.
Search Operation (optional): While not a primary function, searching for an element in a Priority Queue, due to its array-based implementation, has a time complexity of O(n). This is because it may require a linear scan to find a particular element if its priority is unknown.
Considering the time complexities above, Priority Queues prove to be exceptionally beneficial in several use cases:
Task Scheduling: Priority Queues are ideal for managing tasks where certain tasks take precedence over others due to urgency or importance.
Simulation Systems: In simulations where events are processed at varying speeds or frequencies, Priority Queues manage the event schedule effectively, making sure high-priority events are processed first.
Dijkstra’s Algorithm for Shortest Paths: Just like Heaps are used in graph algorithms, Priority Queues are crucial for efficiently finding the shortest path in a weighted graph where the processing order of nodes is determined by their path costs.
Load Balancing and Resource Management: Systems that manage computing resources often utilize Priority Queues to handle jobs according to their resource demands or time constraints.
Real-time Data Processing: In systems where data is processed in real-time, such as stock price updates or sensor data, Priority Queues makes sure that the most critical data is handled promptly.
Priority Queue implementation in Javascript
We will be using ES6 Classes to build our Priority Queue. As mentioned earlier, if we include an “updatePriority” method, we need 2 variations. One would need to involve internal map keeping track of indexes, while the other won’t. Therefore I will be sharing both implementations:
- A simple version that does not utilize a map for tracking element indexes, suitable for smaller data sets or when maximum performance is not critical.
- An optimized version that includes a map to efficiently track and update element indexes, providing faster lookup times which are essential for larger data sets.
Here is the list of methods that we are going to implement:
Simple Priority Queue:
size(): Returns the current number of items in the priority queue.isEmpty(): Determines whether the priority queue is empty.peek(): Retrieves the element with the highest priority (the front of the queue) without removing it.enqueue(value, priority): Inserts a new value with its associated priority into the queue, adjusting the queue to maintain the priority ordering.dequeue(): Removes and returns the element with the highest priority from the queue while preserving the priority order of the remaining elements.updatePriority(value, newPriority, equalityFn): This method allows the priority of an existing element in the queue to be changed. It first locates the element within the queue based on a given value, using theequalityFnto determine equality. If the element is found, its priority is updated to the new value specified. The queue is then reorganized to maintain the correct priority order. This reorganization involves either moving the element up (_heapifyUpFromIndex) if its new priority is higher, or moving it down (_heapifyDownFromIndex) if its new priority is lower compared to its original priority. This makes sure that the queue continuously maintains its priority order even after the priorities of its elements are altered.search(value, equalityFn): (Optional) Locates an element within the queue by its value using a custom equality function, necessary for the non-map-based implementation to update priorities without an external reference.toSortedArray(): (Optional) Returns the heap array in a sorted format. Sorting is based on the type of Heap (Min or Max) the Priority Queue is built upon. A Min Heap based Priority Queue will have the smallest element at the first index, for Max Heap based version is the opposite.
Utility methods:
_parentIndex(i),_leftChildIndex(i),_rightChildIndex(i),_hasLeftChild(i),_hasRightChild(i): Utility methods that assist in navigating the internal heap structure of the priority queue._heapifyUp(),_heapifyDown(): Essential methods for maintaining the heap structure after insertions or deletions, helps to keep the heap property of the queue based on the priority ordering._heapifyUpFromIndex(i),_heapifyDownFromIndex(i): Essential methods for maintaining the heap structure after priority updates, helps to keep the heap property of the queue based on the priority ordering.
Optimized Priority Queue:
Optimized version shares the majority of methods as the simple version, but there are a couple differences with the methods below:
enqueue(value, priority): While adding a new element, the optimized version not only inserts the value into the heap but also updates an internal map. This map tracks the index of each element using its unique ID as the key. This makes sure that the element’s position can be quickly referenced during future operations, providing a significant performance boost for priority updates.
dequeue(): The removal process in the optimized version is augmented by the necessity to maintain the internal map’s accuracy. After the highest priority element is removed from the heap, the map is updated to remove the entry corresponding to this element’s ID. If the last element in the heap is moved to the front (to replace the removed top element), the map is also updated to reflect this new position. This makes sure that subsequent operations on the queue can proceed with the most current information.
updatePriority(id, newPriority): This method in the optimized priority queue is more efficient version for updating the priority of an existing element. The cornerstone of this optimization lies in the use of an internal map (this._map), which stores the indexes of elements in the heap against their unique IDs. When this method is called, it first retrieves the element’s index from the heap using its unique ID, thanks to the map. This approach is significantly more efficient than searching through the entire heap, as it allows for direct access to the element in constant time.
Once the index is obtained, the method checks if the element exists (if the index is not undefined). If the element is found, its priority in the heap is updated to the new value. The queue then needs to adjust to maintain the priority order. This adjustment depends on whether the new priority is higher or lower than the old one. For a higher new priority (a lower numeric value in a min-heap), the element is moved up the heap using _heapifyUpFromIndex. For a lower new priority (a higher numeric value), the method employs _heapifyDownFromIndex to move the element down the heap.
This map-based approach in the optimized priority queue is specially useful with large data sets, or in scenarios where frequent updates to priorities are common.
_generateId(): This method is a private utility function used within the optimized priority queue class. Its purpose is to generate a unique identifier (ID) for each new element added to the queue. It works by maintaining an internal counter (_nextId) that is incremented each time a new ID is required. When called, the method returns the current value of _nextId and then increments the counter. This mechanism provides every element in the queue a distinct ID, which is crucial for efficiently updating an element’s priority in the queue - as this ID is used to quickly locate the element in the internal heap structure. This method is an essential part of the efficiency optimizations in this priority queue implementation.
Priority Queues can be initially challenging to grasp. As mentioned earlier, I would recommend getting familiar with the underlying heap structure that a Priority Queue is built upon — specifically, its array representation. This involves understanding how to identify the parent, left, and right children of any given element using simple array index calculations. Once comfortable with navigating this structure, one should then explore the dynamic nature of Priority Queues, focusing on how the enqueue and dequeue operations work in tandem with heapifyUp and heapifyDown to maintain order according to priority levels.
Additionally, I’ve also included line-by-line explanations for each method in the implementation for you to follow up what is happening in the code. I hope this article helped you to understand what Priority Queues are and how they work! I’d like to encourage you to experiment with the implementations below in your favorite code editor. Thanks for reading!
Simple Priority Queue implementation:
class PriorityQueue {
// The constructor method is called when a new instance of Priority Queue is created.
constructor(comparator) {
// Initialize the heap array.
this.heap = [];
// Set the comparator method for comparing nodes in the heap.
// If no comparator function is provided, it defaults to a comparison
// function that sorts in ascending order (a min-heap).
this.comparator = comparator || ((a, b) => a - b);
}
// Return the number of items in the heap.
size() {
return this.heap.length;
}
// Check if the heap is empty.
isEmpty() {
return this.size() === 0;
}
// Get the top element in the heap without removing it.
// For a min-heap, this will be the smallest element;
// for a max-heap, it will be the largest.
peek() {
return this.heap[0] ? this.heap[0].value : null;
}
// Add a new value to the heap.
enqueue(value, priority) {
// First, add the new value to the end of the array.
this.heap.push({ value, priority });
// Then, move the new value up the heap to its correct position.
this._heapifyUp();
}
// Remove and return the top element in the heap.
dequeue() {
// If the heap is empty, just return null
if (this.isEmpty()) {
return null;
}
// Save the top element so we can return it later
const poppedValue = this.peek();
// If there is more than one node in the heap, move the last node to the top.
const bottom = this.size() - 1;
if (bottom > 0) {
this._swap(0, bottom);
}
// Remove the last node (which is now the top node) from the heap.
this.heap.pop();
// Move the new top node down the heap to its correct position.
this.heapifyDown();
// Finally, return the original top element.
return poppedValue;
}
// This method updates the priority of a specific value in the heap.
updatePriority(value, newPriority, equalityFn) {
// Find the index of the item in the heap that matches the given value.
const index = this.heap.findIndex((item) => equalityFn(item.value, value));
// If the item is not found, exit the function.
if (index === -1) {
return; // Item not found
}
// Update the priority of the found item to the new priority.
const oldPriority = this.heap[index].priority;
this.heap[index].priority = newPriority;
// Re-heapify based on whether the new priority is higher or lower than the old priority.
if (
this.comparator({ priority: newPriority }, { priority: oldPriority }) < 0
) {
// If the new priority is higher, heapify up from the current index.
this._heapifyUpFromIndex(index);
} else {
// If the new priority is lower, heapify down from the current index.
this._heapifyDownFromIndex(index);
}
}
search(value, equalityFn) {
// Find the item in the heap using the provided equality function
const item = this.heap.find((item) => equalityFn(item.value, value));
return item ? item : null;
}
toSortedArray() {
const sortedList = [...this.heap];
return sortedList.sort((a, b) => this.comparator(a.priority, b.priority));
}
// ********************* Helper methods below: *********************
// Method to get the index of a node's parent.
_parentIndex(index) {
/*
About Math.floor:
We take the floor value of the division to
make sure we get the nearest lower integer value.
This is important because array indexes
are integer values and cannot have fractional parts.
*/
return Math.floor((index - 1) / 2);
}
// Method to get the index of a node's left child.
_leftChildIndex(index) {
return 2 * index + 1;
}
// Method to get the value of a node's right child.
_rightChildIndex(index) {
return 2 * index + 2;
}
// Method to check if a node has left child.
// It returns true if the left child index is within the valid range of heap indexes,
// which indicates that a left child exists.
_hasLeftChild(index) {
return this._leftChildIndex(index) < this.size();
}
// Method to check if a node has right child.
// It returns true if the right child index is within the valid range of heap indexes,
// which indicates that a right child exists.
_hasRightChild(index) {
return this._rightChildIndex(index) < this.size();
}
// Method to swap the values of two nodes in the heap.
_swap(i, j) {
// Swap the values of elements at indices i and j without using a temporary variable:
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
}
// This method rearranges the heap after adding a new element.
_heapifyUp() {
// Start with the last element added to the heap
let nodeIndex = this.size() - 1;
// Loop until the node reaches the root or the heap property is maintained
while (
nodeIndex > 0 &&
// Compare the current node with its parent
this.comparator(
this.heap[nodeIndex].priority,
this.heap[this._parentIndex(nodeIndex)].priority
) < 0
) {
// If the current node's priority is higher than its parent, swap them
this._swap(nodeIndex, this._parentIndex(nodeIndex));
// Move to the parent node and continue
nodeIndex = this._parentIndex(nodeIndex);
}
}
// This method rearranges the heap after removing the top element.
_heapifyDown() {
// Start with the root node
let currNodeIndex = 0;
// Loop as long as the current node has a left child
while (this._hasLeftChild(currNodeIndex)) {
// Assume the left child is the smaller child
let smallerChildIndex = this._leftChildIndex(currNodeIndex);
// Check if the right child exists and is smaller than the left child
if (
this._hasRightChild(currNodeIndex) &&
this.comparator(
this.heap[this._rightChildIndex(currNodeIndex)].priority,
this.heap[smallerChildIndex].priority
) < 0
) {
// If so, the right child is the smaller child
smallerChildIndex = this._rightChildIndex(currNodeIndex);
}
// If the current node is smaller than its smallest child, the heap is correct
if (
this.comparator(
this.heap[currNodeIndex].priority,
this.heap[smallerChildIndex].priority
) <= 0
) {
break;
}
// Otherwise, swap the current node with its smallest child
this._swap(currNodeIndex, smallerChildIndex);
// Move to the smaller child and continue
currNodeIndex = smallerChildIndex;
}
}
// This method rearranges the heap upwards from a given index.
_heapifyUpFromIndex(index) {
// Start from the given index
let currentIndex = index;
// Continue as long as the current index is not the root
while (currentIndex > 0) {
// Find the parent index of the current index
let parentIndex = this._parentIndex(currentIndex);
// Compare the current node with its parent
if (
this.comparator(this.heap[currentIndex], this.heap[parentIndex]) < 0
) {
// If current node is smaller than the parent, swap them
this._swap(currentIndex, parentIndex);
// Move to the parent node and continue
currentIndex = parentIndex;
} else {
// If the current node is not smaller than the parent, stop the process
break;
}
}
}
// This method rearranges the heap downwards from a given index.
_heapifyDownFromIndex(index) {
// Start from the given index
let currentIndex = index;
// Continue as long as the current node has a left child
while (this._hasLeftChild(currentIndex)) {
// Assume the left child is the smaller child
let smallerChildIndex = this._leftChildIndex(currentIndex);
// Check if the right child exists and is smaller than the left child
if (
this._hasRightChild(currentIndex) &&
this.comparator(
this.heap[this._rightChildIndex(currentIndex)],
this.heap[smallerChildIndex]
) < 0
) {
// If so, the right child is the smaller child
smallerChildIndex = this._rightChildIndex(currentIndex);
}
// If the current node is smaller or equal to its smallest child, the heap is correct
if (
this.comparator(
this.heap[currentIndex],
this.heap[smallerChildIndex]
) <= 0
) {
break;
}
// Otherwise, swap the current node with its smallest child
this._swap(currentIndex, smallerChildIndex);
// Move to the smaller child and continue
currentIndex = smallerChildIndex;
}
}
}
// Using as MaxPriorityQueue:
class MaxPriorityQueue extends PriorityQueue {
constructor() {
// MaxPriorityQueue uses a comparator that sorts the internal heap in descending order
super((a, b) => b - a);
}
}
// Usage (works as MinPriorityQueue by default)
const priorityQueue = new PriorityQueue();
priorityQueue.enqueue("A", 40);
priorityQueue.enqueue("B", 10);
priorityQueue.enqueue("C", 50);
priorityQueue.enqueue("D", 30);
priorityQueue.enqueue("E", 60);
priorityQueue.enqueue("G", 50);
priorityQueue.enqueue("F", 20);
priorityQueue.toSortedArray();
priorityQueue.updatePriority("A", 5, (a, b) => a === b);
priorityQueue.updatePriority("E", 7, (a, b) => a === b);
priorityQueue.toSortedArray();Optimized Priority Queue implementation:
class PriorityQueue {
// The constructor method is called when a new instance of Priority Queue is created.
constructor(comparator) {
// Initialize the heap array.
this.heap = [];
// Set the comparator method for comparing nodes in the heap.
// If no comparator function is provided, it defaults to a comparison
// function that sorts in ascending order (a min-heap).
this.comparator = comparator || ((a, b) => a - b);
// Map stores internal indexes for more efficient updatePriority
this._map = new Map();
// Counter for the next ID to assign
this._nextId = 0;
}
// Return the number of items in the heap.
size() {
return this.heap.length;
}
// Check if the heap is empty.
isEmpty() {
return this.size() === 0;
}
// Get the top element in the heap without removing it.
// For a min-heap, this will be the smallest element;
// for a max-heap, it will be the largest.
peek() {
return this.heap[0] ? this.heap[0].value : null;
}
// This method adds a new element with its priority into the priority queue.
enqueue(value, priority) {
// Generate a unique identifier for the new element.
const _id = this._generateId();
// Create an entry object containing the value, priority, and the generated ID.
const entry = { value, priority, _id };
// Add the new entry to the end of the heap array.
this.heap.push(entry);
// Store the index of this new entry in the map using its ID for efficient lookups.
// This is important for the updatePriority operation, allowing us to quickly find an element's index.
this._map.set(_id, this.heap.length - 1);
// Reorganize the heap to maintain the heap property after adding a new element.
// This ensures that the heap structure is maintained (either min-heap or max-heap).
this._heapifyUp();
// Return the unique ID of the new entry. This ID can be used later for operations like updatePriority.
return _id;
}
// This method removes and returns the element with the highest priority (at the root of the heap).
dequeue() {
// Check if the heap is empty. If it is, return null.
if (this.isEmpty()) {
return null;
}
// The item to be dequeued is always at the root of the heap (index 0).
const dequeuedItem = this.heap[0];
// Remove the dequeued item's entry from the map using its unique ID.
// This keeps the map updated with only current heap elements.
this._map.delete(dequeuedItem._id);
// Find the index of the last element in the heap.
const bottom = this.size() - 1;
// Check if there are more elements left in the heap after dequeuing.
if (bottom > 0) {
// Replace the root of the heap with the last element.
this.heap[0] = this.heap[bottom];
// Update the position of the moved item in the map.
this._map.set(this.heap[0]._id, 0);
// Remove the last element (now moved to the root) from the heap.
this.heap.pop();
// Reorganize the heap to maintain the heap property after the root change.
this._heapifyDown();
} else {
// If there is only one element in the heap, remove it and clear the map.
this.heap.pop();
this._map.clear();
}
// Return the value of the dequeued item.
return dequeuedItem.value;
}
// This method updates the priority of an element in the priority queue.
updatePriority(id, newPriority) {
// Retrieve the index of the element in the heap using the unique ID from the map.
const index = this._map.get(id);
// If the element with the given ID is not found in the map, exit the function early.
if (index === undefined) {
return;
}
// Retrieve the old priority of the element for comparison.
const oldPriority = this.heap[index].priority;
// Update the priority of the element in the heap with the new priority.
this.heap[index].priority = newPriority;
// Decide whether to heapify up or down based on the new priority.
// If the new priority is higher (smaller value for min-heap), heapify up.
// If the new priority is lower (larger value for min-heap), heapify down.
if (
this.comparator({ priority: newPriority }, { priority: oldPriority }) < 0
) {
this._heapifyUpFromIndex(index);
} else {
this._heapifyDownFromIndex(index);
}
}
search(value, equalityFn) {
// Find the item in the heap using the provided equality function
const item = this.heap.find((item) => equalityFn(item.value, value));
return item ? item : null;
}
toSortedArray() {
const sortedList = [...this.heap];
return sortedList.sort((a, b) => this.comparator(a.priority, b.priority));
}
// ********************* Helper methods below: *********************
// Method to generate unique ID for internal lookup map
_generateId() {
return this._nextId++; // Increment the ID counter and return the new ID
}
// Method to get the index of a node's parent.
_parentIndex(index) {
/*
About Math.floor:
We take the floor value of the division to
make sure we get the nearest lower integer value.
This is important because array indexes
are integer values and cannot have fractional parts.
*/
return Math.floor((index - 1) / 2);
}
// Method to get the index of a node's left child.
_leftChildIndex(index) {
return 2 * index + 1;
}
// Method to get the value of a node's right child.
_rightChildIndex(index) {
return 2 * index + 2;
}
// Method to check if a node has left child.
// It returns true if the left child index is within the valid range of heap indexes,
// which indicates that a left child exists.
_hasLeftChild(index) {
return this._leftChildIndex(index) < this.size();
}
// Method to check if a node has right child.
// It returns true if the right child index is within the valid range of heap indexes,
// which indicates that a right child exists.
_hasRightChild(index) {
return this._rightChildIndex(index) < this.size();
}
// Method to swap the values of two nodes in the heap.
_swap(i, j) {
// Swap the elements in the heap array at indices i and j.
// This is commonly needed during heapify operations to maintain the heap invariant.
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
// After swapping the elements in the heap array, their positions (indices) have changed.
// We must update the map to reflect these new positions.
// Set the map entry for the element that was originally at index i (now at index j)
// to the new index (j). The _id property is used as the key in the map.
this._map.set(this.heap[i]._id, i);
// Similarly, set the map entry for the element that was originally at index j (now at index i)
// to the new index (i). As before, the _id property is used as the key in the map.
this._map.set(this.heap[j]._id, j);
}
// This method rearranges the heap after adding a new element.
_heapifyUp() {
// Start with the last element added to the heap
let nodeIndex = this.size() - 1;
// Loop until the node reaches the root or the heap property is maintained
while (
nodeIndex > 0 &&
// Compare the current node with its parent
this.comparator(
this.heap[nodeIndex].priority,
this.heap[this._parentIndex(nodeIndex)].priority
) < 0
) {
// If the current node's priority is higher than its parent, swap them
this._swap(nodeIndex, this._parentIndex(nodeIndex));
// Move to the parent node and continue
nodeIndex = this._parentIndex(nodeIndex);
}
}
// This method rearranges the heap after removing the top element.
_heapifyDown() {
// Start with the root node
let currNodeIndex = 0;
// Loop as long as the current node has a left child
while (this._hasLeftChild(currNodeIndex)) {
// Assume the left child is the smaller child
let smallerChildIndex = this._leftChildIndex(currNodeIndex);
// Check if the right child exists and is smaller than the left child
if (
this._hasRightChild(currNodeIndex) &&
this.comparator(
this.heap[this._rightChildIndex(currNodeIndex)].priority,
this.heap[smallerChildIndex].priority
) < 0
) {
// If so, the right child is the smaller child
smallerChildIndex = this._rightChildIndex(currNodeIndex);
}
// If the current node is smaller than its smallest child, the heap is correct
if (
this.comparator(
this.heap[currNodeIndex].priority,
this.heap[smallerChildIndex].priority
) <= 0
) {
break;
}
// Otherwise, swap the current node with its smallest child
this._swap(currNodeIndex, smallerChildIndex);
// Move to the smaller child and continue
currNodeIndex = smallerChildIndex;
}
}
// This method rearranges the heap upwards from a given index.
_heapifyUpFromIndex(index) {
// Start from the given index
let currentIndex = index;
// Continue as long as the current index is not the root
while (currentIndex > 0) {
// Find the parent index of the current index
let parentIndex = this._parentIndex(currentIndex);
// Compare the current node with its parent
if (
this.comparator(this.heap[currentIndex], this.heap[parentIndex]) < 0
) {
// If current node is smaller than the parent, swap them
this._swap(currentIndex, parentIndex);
// Move to the parent node and continue
currentIndex = parentIndex;
} else {
// If the current node is not smaller than the parent, stop the process
break;
}
}
}
// This method rearranges the heap downwards from a given index.
_heapifyDownFromIndex(index) {
// Start from the given index
let currentIndex = index;
// Continue as long as the current node has a left child
while (this._hasLeftChild(currentIndex)) {
// Assume the left child is the smaller child
let smallerChildIndex = this._leftChildIndex(currentIndex);
// Check if the right child exists and is smaller than the left child
if (
this._hasRightChild(currentIndex) &&
this.comparator(
this.heap[this._rightChildIndex(currentIndex)],
this.heap[smallerChildIndex]
) < 0
) {
// If so, the right child is the smaller child
smallerChildIndex = this._rightChildIndex(currentIndex);
}
// If the current node is smaller or equal to its smallest child, the heap is correct
if (
this.comparator(
this.heap[currentIndex],
this.heap[smallerChildIndex]
) <= 0
) {
break;
}
// Otherwise, swap the current node with its smallest child
this._swap(currentIndex, smallerChildIndex);
// Move to the smaller child and continue
currentIndex = smallerChildIndex;
}
}
}
// Using as MaxPriorityQueue:
class MaxPriorityQueue extends PriorityQueue {
constructor() {
// MaxPriorityQueue uses a comparator that sorts the internal heap in descending order
super((a, b) => b - a);
}
}
// Usage (works as MinPriorityQueue by default)
// Usage
const priorityQueue = new PriorityQueue();
priorityQueue.enqueue("A", 40);
priorityQueue.enqueue("B", 10);
priorityQueue.enqueue("C", 50);
priorityQueue.enqueue("D", 30);
priorityQueue.enqueue("E", 60);
// keep track of ids:
const idJohn = priorityQueue.enqueue({ message: "hey", name: "john" }, 22);
const idA = priorityQueue.enqueue("F", 20);
console.log("BEFORE:");
priorityQueue.toSortedArray();
console.log("AFTER:");
// Now use the ID to update the priority
priorityQueue.updatePriority(idA, 1);
priorityQueue.updatePriority(idJohn, 55);
priorityQueue.toSortedArray();