Red-Black Trees (RBT) are a type of self-balancing Binary Search Tree (BST) that guarantees logarithmic time complexity for search, insert, and delete operations. This guarantee of consistent performance is a big deal - because regular Binary Search Trees can become unbalanced during insertions and deletions, resulting in a worst-case time complexity of O(n) for search, insert, and delete operations.
Such inefficiency is not suitable for large datasets or applications that demand fast operations. Red-Black Trees solve the problems of standard BSTs by keeping the tree balanced. Which helps to maintain fast and steady performance for all major tasks.
The tone of this article is assuming you are already familiar with Binary Search Trees. If not, I’d recommend you to start from the “Binary Search Tree” article by following the link below, then come back and continue here later:
Deep Dive into Data structures using Javascript - Binary Search Tree
Anatomy of a Red-Black Tree
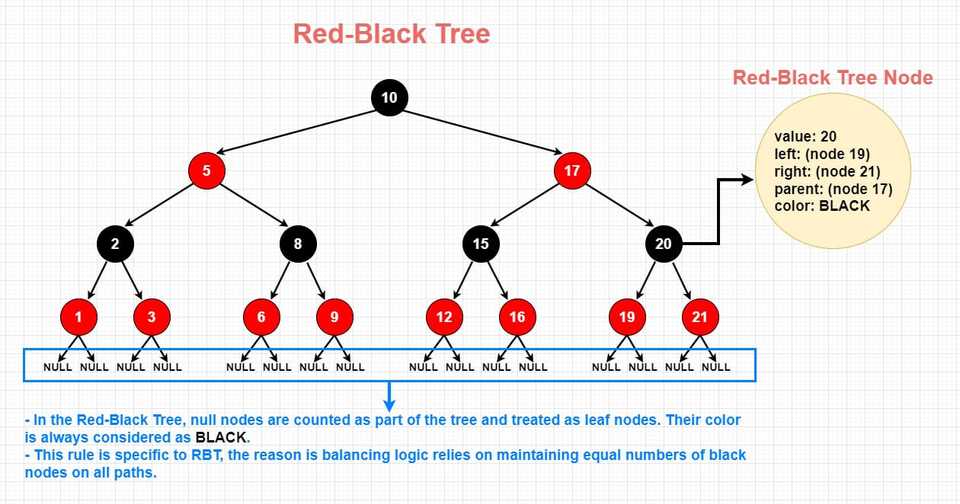
As a variant of BST (Binary Search Tree), Red-Black trees inherit the basic properties of BSTs, such as each node having at most two children, with the left child having a lesser value and the right child having a greater value than their parent node.
What sets Red-Black Trees apart from regular BSTs is their set of additional properties and rules, which ensure that the tree remains balanced after every operation. A balanced tree means having guaranteed logarithmic time complexity for the operations.
Each node in Red-Black Tree consists of 5 properties:
- value: Holds the value / data for the node.
- left: Holds a reference (pointer) to the left child node.
- right: Holds a reference (pointer) to the right child node.
- parent: Holds a reference (pointer) to the parent node.
- color: Holds the color value of the node (red or black).
Additional properties we talk about is the color and parent properties:
Color
Each node in a Red-Black Tree is either red or black. The color property is used to help maintain balance in the tree. By adjusting to a set of rules (Red-Black properties) involving node colors, the tree is kept balanced after every operation.
Parent
Each node in a Red-Black Tree has a pointer to its parent node. This parent property makes it easier to traverse the tree and perform rotations, which are essential for maintaining the Red-Black properties and ensuring balance.
Red-Black Tree rules
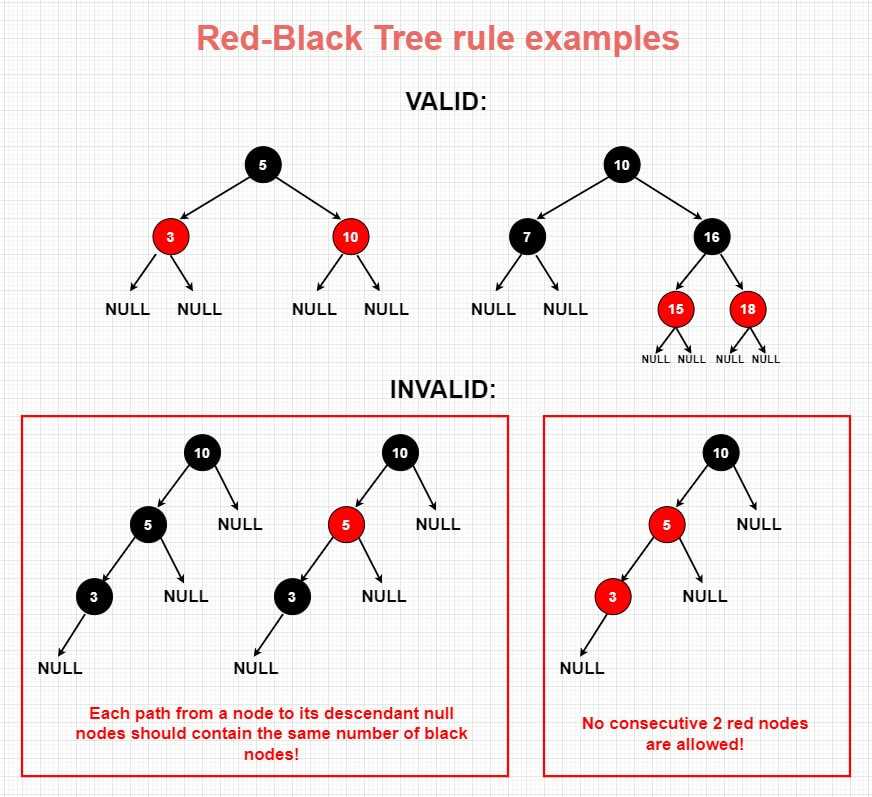
In order to keep the Tree always balanced, the methods needs to follow a set of rules known as Red-Black Tree properties:
- Every node is either red or black: Each node in a Red-Black Tree is either colored red or black.
- The root node is always black: This is a necessary condition to maintain the height-balance property of the Red-Black Tree. If the root node were red, then there would be the possibility of the tree becoming unbalanced when performing insertions and deletions.
- All leaves (null nodes) are considered black: By considering all null nodes as black, we ensure that each path from the root node to a leaf node contains the same number of black nodes.
- No two consecutive red nodes are allowed, i.e., the children of a red node must be black: This is known as the “red node property”. If two red nodes were to appear consecutively, then the tree could become unbalanced when performing insertions and deletions.
- Every path from a node to its descendant null nodes contains the same number of black nodes: This is known as the “black node property”. By ensuring that each path from a node to its descendant null nodes contains the same number of black nodes, height of the tree stays always logarithmic in the number of nodes.
Take a look at the visual below to see how these rules applies to the Red-Black tree:
How does Red-Black Tree stays balanced?
The balance of a Red-Black Tree is maintained through the enforcement of the properties we discussed above. Let’s take a closer look at how these properties contribute to the tree’s balance on a high level:
The color property (red or black) helps to control the height of the tree by preventing consecutive red nodes: This ensures that the path from the root to the farthest leaf is not excessively long, as it prevents the formation of long chains of red nodes.
The black height property guarantees that every path from a node to its descendant null nodes has the same number of black nodes: This ensures that the longest path is no more than twice the length of the shortest path, keeping the tree balanced.
When a new node is inserted or an existing node is deleted, the Red-Black Tree may temporarily violate these properties. To restore the tree’s balance, a series of rotations and color changes, known as “rebalancing operations,” are performed. These operations preserve the Red-Black Tree properties to keep the tree balanced after every modification.
When to use Red-Black Tree
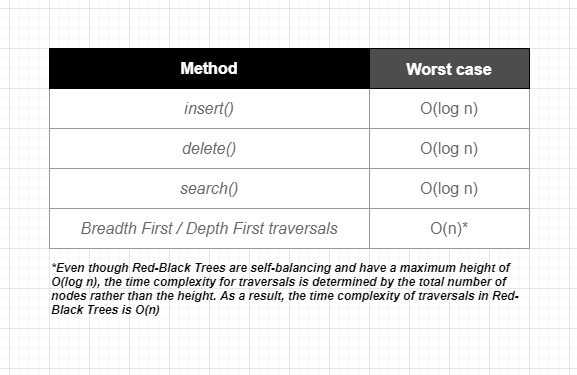
Let’s start with taking a look at the Big O of common operations in Red-Black Tree:
Since the Tree always stays balanced and maintains the height of O(log n), time complexity for all crucial operations such as insert, delete and search is always O(log n) without edge cases. This is a significant advantage over Binary Search Trees as they can become unbalanced, which leads to a worst-case time complexity of O(n) for these operations.
When it comes to breadth-first and depth-first traversals, they have a time complexity of O(n) (linear time), just like for any other type of tree. Despite Red-Black Trees being self-balancing with a maximum height of O(log n), the time complexity of traversals is determined by the total number of nodes rather than the height. Therefore the time complexity of traversals in Red-Black Trees is also O(n).
The efficiency with insert / delete / search operations makes Red-Black Trees powerful tool in certain scenarios, specifically when dealing with large datasets and requiring efficient operations. Some use cases where Red-Black Trees would make sense:
Efficient Search Operations: In scenarios when data retrieval is frequent and critical, Red-Black Trees provide significant benefits. Integrating this data structure into database indexing or object-oriented databases can greatly enhance the speed of search queries.
For example, consider a large online bookstore with millions of books in its inventory. Whenever a customer searches for a book on the website, the system needs to quickly retrieve the relevant book information from the database and display the results.
By using a Red-Black Tree as an indexing structure, the bookstore can store information about each book in a sorted manner based on a key, such as the book’s title or author. As a result, the bookstore can efficiently retrieve the book information, providing the customer with faster search results. This not only improves the user experience but also reduces the load on the database server, as it can process search queries more efficiently using the Red-Black Tree indexing structure.
Dynamic Data Handling: When working with dynamic datasets where insertions and deletions are a regular occurrence, Red-Black Trees demonstrate their strength. Consider an online trading platform, where users can buy and sell stocks. This platform handles a high volume of buy and sell orders from users in real-time. Red-Black Trees can be used to efficiently manage and process these orders.
When a user places a buy or sell order, the trading platform can leverage Red-Black Trees to keep the orders sorted based on price or other relevant criteria. For example, when a user wants to execute a buy order, the platform can efficiently find the best available sell order(s) at the lowest price by traversing the Red-Black Tree. Similarly, when a user wants to execute a sell order, the platform can identify the highest bid(s) from the buy orders in the Red-Black Tree.
The use of Red-Black Trees enables the trading platform to quickly match buyers with sellers, ensuring efficient and accurate order execution. The balanced nature of the Red-Black Tree allows for fast search operations and makes it easier to identify the most favorable buy or sell orders.
Ordered Data Operations: In use cases where it’s crucial to maintain an ordered sequence of elements, Red-Black Trees are an ideal choice. For instance, in a time-series database where data is organized by timestamps, Red-Black Trees can ensure chronological order while maintaining quick insertion and deletion times.
Consider a social media platform that stores posts from users in a time-series database. Each post is associated with a timestamp indicating when it was created. In this scenario, Red-Black Trees can be utilized to efficiently handle the ordered sequence of posts.
By using Red-Black Trees as the underlying data structure, the social media platform can ensure that the posts are stored in chronological order based on their timestamps. This allows for easy retrieval and display of posts in the correct sequence.
When a user creates a new post, the platform can leverage the Red-Black Tree to quickly insert the post into the appropriate position, maintaining the chronological order. Similarly, if a user deletes a post, the Red-Black Tree enables efficient removal of the post while preserving the ordering of the remaining posts.
With the help of Red-Black Trees, the social media platform can provide users with a seamless browsing experience. Users can easily navigate through posts in the correct time order, whether they are scrolling through their own timeline or exploring posts from other users.
Language Libraries: Red-Black Trees are commonly used in the standard libraries of numerous programming languages. For instance, C++ uses Red-Black Trees in its STL (Standard Template Library) for map and set data structures, providing an efficient implementation for these abstractions.
Database Systems: Databases often use Red-Black Trees for indexing. These data structures provide fast access, allowing the database to retrieve records swiftly. This is especially important when handling complex queries that involve multiple attributes and require optimal performance.
Even though Red-Black Trees are very versatile, they are not a “one-size-fits-all” solution. Depending on the specific requirements of your system, other data structures may be more suitable. The key is to understand the nature of your problem and the operations you need to perform frequently, then choose the most suitable data structure accordingly.
Red-Black Tree vs AVL Tree
If you find yourself in a situation where you might want to use Red-Black Trees, most likely you’ll be looking for a self-balancing Binary Search Tree variation. There are various self-balancing trees, but Red-Black Tree and AVL Tree are the most common options.
Even though both of them are self-balancing, one is preferred over the other in certain cases.
Choose a Red-Black Tree when:
- Insertions and Deletions are Frequent: The process of balancing a Red-Black Tree after insertions and deletions is generally faster than that of an AVL tree due to fewer rotations, making it a better choice for write-heavy workloads.
- Memory is a Concern: Red-Black Trees usually require less space than AVL trees because they only need to store one bit of information (the color) at each node.
- Moderate Search Times are Acceptable: While RBTs do ensure an upper bound of O(log n) for search times, AVL trees generally offer faster lookups due to their stricter balancing. If your application can tolerate slightly longer search times in favor of faster writes or less memory usage, an RBT may be a good choice.
Choose an AVL Tree when:
- Lookups are Frequent: AVL trees are more strictly balanced than Red-Black Trees, which means that they generally provide faster lookup times. If your application involves many more read operations than write operations, an AVL tree could be a better choice.
- Consistently Quick Search Times are Crucial: If your use case requires consistently fast search times and the frequency of updates (insertions and deletions) is relatively low, an AVL tree would be a more suitable choice.
- Insertions and Deletions are Infrequent: While AVL trees can be slower to update than Red-Black Trees, this may not be a significant factor if updates are relatively rare in your application.
At the end, the choice between Red-Black Trees and AVL trees often comes down to the specific needs of your application, including the relative frequency of different operations, the importance of quick search times and memory usage constraints.
Red-Black Tree implementation in Javascript
We will be using ES6 Classes to build our Red-Black Tree. Here is the list of methods we are going to implement:
insert(value)- This method is used to insert a new value into the Red-Black Tree. The method starts by creating a new node and placing it in the correct position, like in a standard Binary Search Tree. After the node is inserted, the _insertFixup method is called to restore the Red-Black Tree properties._insertFixup(node)- This is a helper method used to ensure that the Red-Black Tree properties are maintained after an insertion operation. The method adjusts the color of nodes and performs rotations as needed until the tree is balanced and follows the Red-Black Tree rules.delete(value)- This method removes a node with a given value from the tree. It first finds the node using the search method, then removes it while maintaining the Red-Black Tree properties. After the node is deleted, the _deleteFixup method is called to restore the Red-Black Tree properties._deleteFixup(node)- This is a helper method used to ensure that the Red-Black Tree properties are maintained after a deletion operation. Similar to the _insertFixup method, it adjusts the color of nodes and performs rotations as needed until the tree is balanced and follows the Red-Black Tree rules.search(value)- This method finds a node in the tree that matches a given value. It’s used during the delete operation to find the node that needs to be removed._replaceParent(curNode, newNode)- This helper method is used to replace the parent of a given node with a new node. It’s used during rotations and node deletions._leftRotation(node) and _rightRotation(node)- These are helper methods used to perform left and right rotation algorithms on the tree. They’re used during the insert and delete operations to maintain the Red-Black Tree properties._flipColor(node)- A helper method that changes the color of a node and its children. It is used during insert and delete operations to maintain the Red-Black Tree properties._isRed(node)- A helper method that checks if a node is red. This method is used in various operations to determine the color of a specific node.findMin(node)- This method finds the node with the smallest value in the tree. It’s used during the delete operation to find the successor of a node that’s being deleted.levelOrderTraversal()- Display the Red-Black Tree as a level-order multi-dimensional array, using the “level order traversal”. The final output array will represent the tree with each sub-array representing a level of the tree.
I’d like to note understanding Red-Black Trees for the first time will be a solid challange, because they reside at the advanced and complex end of the Data structures spectrum. Fully grasping all the concepts will require investing time into experimentation and exploration. The power of Red-Black Tree lays within the “maintaining balance” factor (which is the key concept) - but it comes at the cost of implementation complexity.
When you study insertion and deletion methods, you’ll be looking at a lot of conditions and steps - which are combined with Red-Black Tree specific operations such as rotations and color flipping. Understanding these operations is crucial, as they form the core mechanics of how a Red-Black Tree maintains its balance during insertions and deletions.
Rotations (left and right) and color flipping are the key operations that help to re-balance the tree whenever its properties are violated due to an insertion or a deletion. They work together to rearrange the nodes and change their colors to restore the properties of the Red-Black Tree. Starting with having a good understanding of how these operations work will make it easier to understand the more complex insertion and deletion methods.
To visualize and better understand the mechanics of the Red-Black Tree, I highly recommend playing around with this amazing Red-Black Tree Visualizer at the link down below:
I hope this article helped you to give a good foundation on what Red-Black Trees are and how they work! I’d like to encourage you to experiment with the implementation below in your favorite code editor. Thanks for reading!
Implementation of Red-Black Tree in Javascript
const NodeColor = {
RED: 'RED',
BLACK: 'BLACK',
}
class RBTNode {
constructor(value, parent = null) {
this.value = value
this.left = null
this.right = null
this.parent = parent
this.color = NodeColor.RED
}
}
class RedBlackTree {
constructor() {
this.root = null
}
insert(value) {
// Define an inner helper function for the recursive insertion
const insertHelper = (node) => {
// The current node we're considering
const currNode = node
// If the value to insert is less than the value of the current node
if (value < currNode.value) {
// If a left child node exists, recursively call 'insertHelper' on it
if (currNode.left) {
insertHelper(currNode.left)
} else {
// If no left child node exists, create a new node with the value
// Make the new node a left child of the current node
// The color of the new node is red by default (from the RBTNode constructor)
currNode.left = new RBTNode(value)
// Set the parent of the new node to be the current node
currNode.left.parent = currNode
// Call the helper method '_insertFixup' to maintain Red-Black Tree properties after insertion
this._insertFixup(currNode.left)
}
} else if (value > currNode.value) {
// If the value to insert is greater than the value of the current node
// If a right child node exists, recursively call 'insertHelper' on it
if (currNode.right) {
insertHelper(currNode.right)
} else {
// If no right child node exists, create a new node with the value
// Make the new node a right child of the current node
// The color of the new node is red by default (from the RBTNode constructor)
currNode.right = new RBTNode(value)
// Set the parent of the new node to be the current node
currNode.right.parent = currNode
// Call the helper method '_insertFixup' to maintain Red-Black Tree properties after insertion
this._insertFixup(currNode.right)
}
}
// If the value is equal to the current node's value, we do nothing because
// duplicates are not typically allowed in binary search trees
}
// If the tree is empty (no root node)
if (!this.root) {
// Create a new root node with the value
// The color of the new root node is red by default (from the RBTNode constructor)
this.root = new RBTNode(value)
// Call the helper method '_insertFixup' to maintain Red-Black Tree properties after insertion
// In this case, it will simply recolor the root to black
this._insertFixup(this.root)
} else {
// If the tree is not empty, call the 'insertHelper' function on the root node
insertHelper(this.root)
}
}
// Helper method to maintain tree balance after an insertion
_insertFixup(node) {
// Start with the node that was just inserted
let currNode = node
// While the parent of the current node is red and the grandparent exists
// This loop maintains the property that no two red nodes will be adjacent
while (this._isRed(currNode.parent) && currNode.parent.parent) {
// Define some helper variables to make the code more readable
const { parent } = currNode
const grandparent = parent.parent
// If the parent of the current node is a left child
if (parent === grandparent.left) {
// If the uncle (the right child of the grandparent) is red
if (this._isRed(grandparent.right)) {
// Flip the colors of the parent, grandparent, and uncle
// This maintains the property that every path from a node to its descendant leaves contains the same number of black nodes
this._flipColor(grandparent)
} else {
// If the uncle is black or null
// If the current node is a right child, do a left rotation to make it a left child
// This is done to prevent two red nodes from being adjacent
if (currNode === parent.right) {
this._leftRotation(parent)
// After the rotation, the current node and its parent are swapped
currNode = parent
}
// Perform a right rotation on the grandparent
// This makes the former parent (a red node) the parent of its former parent (a black node)
// This maintains the property that every path from a node to its descendant leaves contains the same number of black nodes
this._rightRotation(grandparent)
}
} else {
// The mirror case when the parent of the current node is a right child
// The code is the same except that 'left' and 'right' are exchanged
if (this._isRed(grandparent.left)) {
this._flipColor(grandparent)
currNode = grandparent
} else {
if (currNode === parent.left) {
this._rightRotation(parent)
currNode = parent
}
this._leftRotation(grandparent)
}
}
// Move up the tree
currNode = grandparent
}
// Ensure the root is always black to maintain the black-root property
this.root.color = NodeColor.BLACK
}
delete(value, node = this.root) {
// Search the tree to find the target node
const targetNode = this.search(value, node)
// If the target node is not found, return false
if (!targetNode) {
return false
}
// If the target node has no children (leaf node)
if (!targetNode.left && !targetNode.right) {
// If the target node is red, simply remove it by replacing it with null in its parent
// Red nodes can be removed freely because removing them doesn't affect the black height property
if (this._isRed(targetNode)) {
this._replaceParent(targetNode, null)
} else {
// If the target node is black, removal would affect black height property
// Hence, we need to call '_deleteFixup' to fix the potential violations
this._deleteFixup(targetNode)
// After that, we can remove the black node
this._replaceParent(targetNode, null)
}
} else if (!targetNode.left || !targetNode.right) {
// If the target node has only one child (unilateral subtree)
if (targetNode.left) {
// If the child is on the left, set the child's color to black
// The color is set to black to maintain the black height property
targetNode.left.color = NodeColor.BLACK
// Update the parent pointer of the child
targetNode.left.parent = targetNode.parent
// Replace the target node with its child
this._replaceParent(targetNode, targetNode.left)
} else {
// Similar operations for the right child
targetNode.right.color = NodeColor.BLACK
targetNode.right.parent = targetNode.parent
this._replaceParent(targetNode, targetNode.right)
}
} else {
// If the target node has two children
// Find the node with the smallest value that is larger than the value of the target node (aux)
// This node is used to replace the target node
const aux = this.findMin(targetNode.right)
// Replace the value of the target node with the value of the aux node
targetNode.value = aux.value
// Delete the aux node recursively
// The aux node will have at most one child, so this deletion is easier
this.delete(aux.value, targetNode.right)
}
// Return the root of the tree after deletion
return this.root
}
// Helper method to maintain tree balance after a deletion
_deleteFixup(node) {
// 'currNode' is the node to be fixed
let currNode = node
// Loop until 'currNode' is the root or 'currNode' is red
while (currNode !== this.root && !this._isRed(currNode)) {
// Get the parent of 'currNode'
const { parent } = currNode
// Define 'sibling', which will be the sibling of 'currNode'
let sibling
// If 'currNode' is a left child
if (currNode === parent.left) {
// 'sibling' is the right child of 'parent'
sibling = parent.right
// If the 'sibling' is red
if (this._isRed(sibling)) {
// Perform left rotation on 'parent'
this._leftRotation(parent)
}
// If both children of 'sibling' are black
else if (!this._isRed(sibling.left) && !this._isRed(sibling.right)) {
// If 'parent' is red
if (this._isRed(parent)) {
// Swap colors of 'parent' and 'sibling'
parent.color = NodeColor.BLACK
sibling.color = NodeColor.RED
// Fixup is done because 'currNode' now has an additional black link
break
}
// If 'parent' is black, make 'sibling' red
sibling.color = NodeColor.RED
// Move up the tree
currNode = parent
}
// If 'sibling's left child is red and right child is black
else if (this._isRed(sibling.left) && !this._isRed(sibling.right)) {
// Perform right rotation on 'sibling'
this._rightRotation(sibling)
}
// If 'sibling's right child is red
else {
// Perform left rotation on 'parent'
this._leftRotation(parent)
// Change color of 'parent' and 'sibling's right child to black
parent.color = NodeColor.BLACK
sibling.right.color = NodeColor.BLACK
// Fixup is done because 'currNode' now has an additional black link
break
}
}
// If 'currNode' is a right child, similar operations are performed with 'left' and 'right' interchanged
else {
sibling = parent.left
if (this._isRed(sibling)) {
this._rightRotation(parent)
} else if (!this._isRed(sibling.left) && !this._isRed(sibling.right)) {
if (this._isRed(parent)) {
parent.color = NodeColor.BLACK
sibling.color = NodeColor.RED
break
}
sibling.color = NodeColor.RED
currNode = parent
} else if (this._isRed(sibling.right) && !this._isRed(sibling.left)) {
this._leftRotation(sibling)
} else {
this._rightRotation(parent)
parent.color = NodeColor.BLACK
sibling.left.color = NodeColor.BLACK
break
}
}
}
}
search(value, node = this.root) {
// Check if the current node is null (reached a leaf node or an empty tree)
if (!node) {
// Value not found, return false
return false
}
// Check if the current node's value matches the search value
if (value === node.value) {
// Value found, return the node
return node
}
// If the search value is less than the current node's value, go to the left subtree
if (value < node.value) {
// Recursively call the search function on the left child node
return this.search(value, node.left)
}
// If the search value is greater than the current node's value, go to the right subtree
// This assumes the tree follows the convention of left child nodes having lesser values and right child nodes having greater values
return this.search(value, node.right)
}
/*
This method is used to replace the parent of a given node with a new node. It is primarily used during node deletion and rotation operations. When a node is deleted or when rotations are performed, it may be necessary to update the parent reference of a child node to point to a new node.
*/
_replaceParent(currNode, newNode) {
// Get the parent node of the current node
const { parent } = currNode
// Check if the current node is the root node (no parent)
if (!parent) {
// If so, set the new node as the new root of the tree
this.root = newNode
}
// If the current node is the left child of its parent
else if (currNode === parent.left) {
// Set the new node as the left child of the parent
parent.left = newNode
}
// If the current node is the right child of its parent
else {
// Set the new node as the right child of the parent
parent.right = newNode
}
}
/*
A helper method that performs a left rotation on the tree structure.
Left rotation is an operation that repositions the nodes in the tree
to maintain its properties when they have been disturbed, for example, during insertion or deletion.
It is used when the right child of a node is colored red. The operation involves repositioning
the node and its right child, and updating the colors of the nodes accordingly. After a left rotation, the
former parent becomes the left child of its former right child.
This method should be called when it is safe to do a left rotation, that is, when the right child is not null.
*/
_leftRotation(node) {
// 'currNode' is set as the right child of 'node'
const currNode = node.right
// The left child of 'currNode' becomes the right child of 'node'
node.right = currNode.left
// 'node' becomes the left child of 'currNode'
currNode.left = node
// The color of 'currNode' is set as the color of 'node'
currNode.color = node.color
// The color of 'node' is set as red
node.color = NodeColor.RED
// The parent of 'node' is replaced with 'currNode'
this._replaceParent(node, currNode)
// The parent of 'currNode' is set as the parent of 'node'
currNode.parent = node.parent
// 'node' becomes the child of 'currNode'
node.parent = currNode
// If 'node' has a right child, the parent of the right child is set as 'node'
if (node.right) {
node.right.parent = node
}
}
/*
A helper method that performs a right rotation on the tree structure.
Right rotation is an operation that repositions the nodes in the tree
to maintain its properties when they have been disturbed, for example, during insertion or deletion.
It is used when the left child of a node is colored red. The operation involves repositioning
the node and its left child, and updating the colors of the nodes accordingly. After a right rotation, the
former parent becomes the right child of its former left child.
This method should be called when it is safe to do a right rotation, that is, when the left child is not null.
*/
_rightRotation(node) {
// 'currNode' is set as the left child of 'node'
const currNode = node.left
// The right child of 'currNode' becomes the left child of 'node'
node.left = currNode.right
// 'node' becomes the right child of 'currNode'
currNode.right = node
// Update color: The color of 'currNode' is set as the color of 'node'
currNode.color = node.color
// The color of 'node' is set as red
node.color = NodeColor.RED
// Update parent node: The parent of 'node' is replaced with 'currNode'
this._replaceParent(node, currNode)
// The parent of 'currNode' is set as the parent of 'node'
currNode.parent = node.parent
// 'node' becomes the child of 'currNode'
node.parent = currNode
// If 'node' has a left child, the parent of the left child is set as 'node'
if (node.left) {
node.left.parent = node
}
}
/*
Helper method that changes the color of a node and its children.
The concept here is to change the color of the parent node to red, and the color of the two child nodes to black.
This color flip is part of the process that helps to maintain the properties of a Red-Black Tree, which include keeping the tree balanced and ensuring that no two red nodes are adjacent, among others.
Please note that before calling this method, you should check that both children of the node are present and their colors are red. This method assumes this condition is met.
*/
_flipColor(node) {
// The color of the current node is set to RED
node.color = NodeColor.RED
// The color of the left child of the current node is set to BLACK
node.left.color = NodeColor.BLACK
// The color of the right child of the current node is set to BLACK
node.right.color = NodeColor.BLACK
}
// Helper method to check the node color
_isRed(node) {
return node ? node.color === NodeColor.RED : false
}
// Helper method that finds the node with the smallest value in the tree. It's used during the delete operation to find the successor of a node that's being deleted.
findMin(node = this.root) {
let currentNode = node
while (currentNode && currentNode.left) {
currentNode = currentNode.left
}
return currentNode
}
// Displays an array that will represent the tree
// in level-order, with each sub-array representing a level of the tree.
levelOrderTraversal() {
// Create an empty array to store the traversed nodes
const temp = []
// Create an array to keep track of the current level of nodes
const queue = []
// If the tree has a root, add it to the queue
if (this.root) {
queue.push(this.root)
}
// Keep traversing the tree while there are nodes in the queue
while (queue.length) {
// Create an array to store the nodes of the current level
const subTemp = []
// Store the number of nodes in the current level
const len = queue.length
// Iterate through the current level of nodes
for (let i = 0; i < len; i += 1) {
// Dequeue the first node in the queue
const node = queue.shift()
// Push the node's value to the subTemp array
subTemp.push(node.value)
// If the node has a left child, add it to the queue
if (node.left) {
queue.push(node.left)
}
// If the node has a right child, add it to the queue
if (node.right) {
queue.push(node.right)
}
}
// Push the subTemp array to the temp array
temp.push(subTemp)
}
// Return the final temp array
return temp
}
}
export default RedBlackTree